VVT9 - Transient temperature in a semi-infinite solid
| Solution | Test case | ||
|---|---|---|---|
| Finite volume method | Case A: Temperature constraint | SVTEST11 | |
| Case B: Heat flux load | SVTEST12 | ||
| Finite element method | Case A: Temperature constraint | SVTEST237 | |
| Case B: Heat flux load | SVTEST238 | ||
Description
The purpose of this test case is to determine the transient temperature at a depth of 0.025 m in a semi-infinite solid for specified boundary conditions. The model is a one-dimensional problem, thus a single elements row can be used to model the semi-infinite solid.
Geometry
A solid geometry part is created by extruding a 5 mm by 5 mm square cross-section to a length of L = 200 mm.
Simulation model
The regular mesh is made of forty 5 x 5 x 5 mm3 hexahedral solid elements along the length of the extrusion. The ends of the extrusion are selected as the source and target faces. The element size of 5 mm is specified.
The meshed elements have the following material and physical properties:
- Mass density: ρ = 7800 kg/m3
- Thermal conductivity: k = 45 W/m·°C
- Specific heat at constant pressure: Cp = 412 J/kg·°C
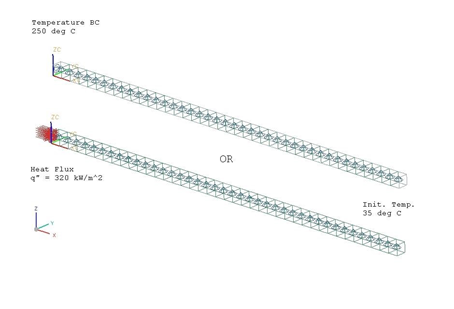
The following boundary conditions are applied:
- Initial Conditions constraint: Initial Temperature on the solid geometry for both case A and B with a value of Ti =35 ºC.
- Temperature constraint (case A) on the end of the solid (case A) with a value of To= 250 °C.
- Thermal loads: Heat flux (case B) on the end of the solid with a value of q'' = 320000 W/m2 .
The following solution options are set:
- Solution Type=Transient (model is simulated for 30 seconds, with 100 time steps and 10 results samples).
The default solver parameters are selected.
Theory
The partial differential equation for the temperature distribution, T(x,t) in the semi-infinite solid is
where = 1.4 × 10−5 in2/s.
In Case A, the boundary and initial conditions are
and the solution is
In Case B, the boundary and initial conditions are
and the solution is
Results
The following table compares the temperature predicted by the theoretical calculation and computed by the thermal solver at x = 0.025 m and t = 30 seconds for both cases. Simulation results are in agreement with theoretical values.
| Finite volume method | Finite element method | ||||
|---|---|---|---|---|---|
| Case | Ttheory (ºC) | Tsim (ºC) | Error (%) | Tsim (ºC) | Error (%) |
| A | 118.6 | 118.9 | 0.25 | 118.76 | 0.13 |
| B | 79.2 | 80.07 | 1.09 | 79.05 | 0.20 |
