VVT4 - Kershaw test
| Solution | Test case | ||
|---|---|---|---|
| Finite volume method | Steady state | SVTEST4 | |
| Transient | SVTEST5 | ||
| Finite element method | Steady state | SVTEST230 | |
| Transient | SVTEST231 | ||
Description
The purpose of this test case is to determine the transient temperature response for a 1 m × 1 m plate with a non-regular mesh and fixed temperatures on the top and bottom edges.
Geometry
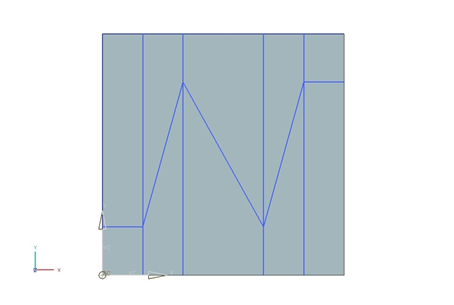
A 1 m × 1 m extrusion is created. A sketch is drawn in order to subdivide the face for the irregular mesh as shown in the following figure.
Simulation model
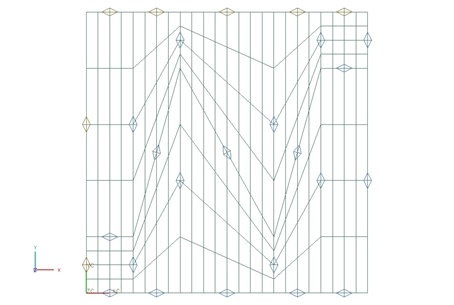
The mapped mesh is made of quadrilateral thin shell elements to generate the irregular mesh as shown in the following figure. The number of elements per side of the face are specified.
The meshed elements have the following material and physical properties:
- Thickness: 1 mm
- Mass density: ρ = 1 kg/m3
- Thermal conductivity: k = 1 W/m·K
- Specific heat at constant pressure: Cp = 1 J/kg·K
The following boundary conditions are applied:
- Temperature constraint on the one edge of the square face with a value of T 1 = 100 ºC.
- Temperature constraint on the other edge of the square face with a value of T2 = 0 ºC.
The default solution options and solver parameters are selected.
Theory
A Kershaw mesh is simply a plate element mesh of a 1 unit by 1 unit area in which the shape of created elements range from square to extremely skewed polygons. A solver which correctly calculates the plate element resistance’s will show equally spaced isotherms parallel to the constrained sides. Therefore, the temperature results should not be a function of the mesh generated or the shape of the elements.
Results
The following figures display isotherms parallel to the constrained edges that are only negligibly affected by the element shapes for the times of t=0.005 s, t=0.05 s, t =0.5 s, and t=5 s.

