VVT14 - Hollow cylinder with convective boundary conditions
| Solution | Test case |
|---|---|
| Finite volume method | SVTEST18 |
| Finite element method | SVTEST244 |
Description
The purpose of this test case is to determine the temperature distribution through the thickness of a hollow cylinder by convective heat transfer.
Geometry
The hollow cylinder is defined with an inner diameter of 600 mm and an outer diameter of 780 mm. The axisymmetric modeling technique is used, which requires the sketch on the XZ plane. Cylinder thickness is 50 mm, therefore a plate is sketched with the length of 50 mm and height of 10 mm, starting from the inner diameter of the cylinder. A bounded plane was attached to this plate.
Simulation model
This model uses the Axisymmetric Thermal solution type.
A 2D mesh of quadrilateral thin shell elements is generated on the surface of the plate, using 30 mm element size.
The meshed elements have the following material and physical properties:
- Thermal conductivity: k = 40 W/m·°C
- Mass density: ρ = 1kg/m3
- Thickness: not required for the axisymmetric thermal analysis
The following boundary conditions are applied:
- Convection to Environment constraint on the inside edge of the cylinder with a heat transfer coefficient hi = 150 W/m2·°C and an environment temperature Ti = 500 ºC.
- Convection to Environment constraint on the outside edge of the cylinder with a heat transfer coefficient ho = 142 W/m2·°C and an environment temperature To = 20 ºC.
The following figure shows the mesh and the location of the convective boundary conditions.
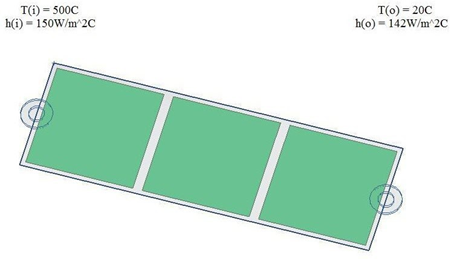
The following solution options are set:
- Solution Type = Steady State
- Results Options: Select the heat flux and temperature at nodes and elements
The default solver parameters are selected.
Theory
The heat transfer rates by conduction through the cylinder thickness and by convection along the inside surface of the hollow cylinder is determined [4], [5], [6] using the following equations:
From these results, the inner surface temperature is determined using the following equations:
From these results, the outer surface temperature is determined using the following equations:
Results
The following table compares the node temperatures computed by the thermal solver with theoretical values.
| Finite volume method | Finite element method | ||||
|---|---|---|---|---|---|
| Parameter | Ttheory (ºC) | Tsim (ºC) | Error (%) | Tsim (ºC) | Error (%) |
| Ti | 272.35 | 272.30 | 0.02 | 272.246 | 0.038 |
| T0 | 204.50 | 205.00 | 0.24 | 205.066 | 0.277 |
The following table shows the heat transfer rates by conduction through the cylinder thickness.
| Finite volume method | Finite element method | |||
|---|---|---|---|---|
| Rcyl (mm) | qr, (W/m) | Error (%) | qr, (W/m) | Error (%) |
| 315 | 64535.88 | 0.26 | 64395.36 | 0.046 |
| 345 | 64512.89 | 0.23 | 64395.83 | 0.047 |
| 375 | 64493.76 | 0.20 | 64394.80 | 0.045 |
