VVT1 - Conduction through a multi-layer cylinder
| Solution | Test case |
|---|---|
| Finite volume method | SVTEST1 |
| Finite element method | SVTEST227 |
Description
The purpose of this test case is to determine the radial temperature distribution through a hollow steel pipe and its surrounding insulation.
Geometry
The cylinder slice is modeled with a height of 5 mm. Half of the cross-section (in the x-z plane) of the segment is modeled, because of axisymmetry. The inner edge of the cross-section is located at r1 = 10 mm from the center of the cylinder. The outer edge is at r3 = 50 mm. The cross-section is revolved to create a solid body. A datum plane is offset 10 mm from the inner edge of the cross-section to split the front face of the revolved solid. This split represents the interface between the steel and the insulation and located at r2 = 20 mm.
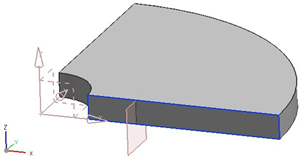
Simulation model
Because this model uses the Axisymmetric Thermal solution type, the front surface of the revolved solid is meshed using quadrilateral elements. A mapped mesh is applied to each section of the front surface so that each element is 5 mm by 5 mm in area.
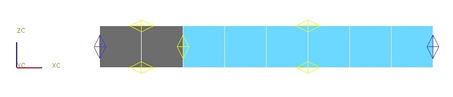
The meshed elements have the following material and physical properties:
- The two inner elements:
- Material: Steel
- Thermal conductivity: k = 19 W/m·K
- The two outer elements:
- Material: Asbestos
- Thermal conductivity: k = 0.2 W/m·K
The following boundary conditions are applied:
- Temperature constraint on the inner edge of the front surface with a value of T1 = 600 °C
- Temperature constraint on the outer edge with a value of T3 = 100 °C

The following solution options are set:
- Solution Type = Steady State
- Results Options: Select the conductive heat fluxes at nodes and elements
The default solver parameters are selected.
Theory
The thermal resistance of a cylindrical shell [1] is given by:
where:
- ri is the inner radius.
- ro is the outer radius.
- L is the length of the cylinder.
- k is the thermal conductivity of the material.
The thermal resistance per unit length for the steel (s) and asbestos (a) cylinders for the arbitrary length are defined as:
The thermal resistance network consists of the series network, therefore, the rate of the heat transfer radially through the cylinders is constant, calculated as follows:
The temperature can then be calculated for a given radial distance as follows:
Results
The following table compares the temperature distribution obtained from the theoretical calculation with the nodal temperatures obtained from the thermal solver using finite volume and finite element methods. Simulation results are in agreement with theoretical values.
| Finite volume method | Finite element method | ||||
|---|---|---|---|---|---|
| r (m) | Ttheory (°C) | Tsim (°C) | Error (%) | Tsim (°C) | Error (%) |
| 0.0100 | 600.00 | 600.00 | 0.00 | 600.00 | 0.00 |
| 0.0150 | 597.69 | 597.86 | 0.03 | 597.72 | 0.00 |
| 0.0200 | 596.05 | 596.23 | 0.03 | 596.08 | 0.01 |
| 0.0250 | 475.25 | 480.77 | 1.16 | 475.49 | 0.05 |
| 0.0300 | 376.54 | 380.36 | 1.01 | 376.82 | 0.07 |
| 0.0350 | 293.09 | 295.88 | 0.95 | 293.33 | 0.08 |
| 0.0400 | 220.80 | 222.93 | 0.97 | 220.97 | 0.08 |
| 0.0450 | 157.04 | 158.72 | 1.07 | 157.12 | 0.05 |
| 0.0500 | 100.00 | 100.00 | 0.00 | 100.00 | 0.00 |
The following table shows that the radial heat transfer rate per unit height (qr) obtained from the elemental heat fluxes, calculated by the thermal solver with the finite volume method, is not constant. This is due to the mesh coarseness. A second trial run, using more elements in the radial direction, reduces this flux error. The finite element methods provides constant results for the radial heat transfer rate per unit height (qr) and a better accuracy in comparison with finite volume method results for coarse mesh.
| Finite volume method | Finite element method | |||||
|---|---|---|---|---|---|---|
| r (m) | qr, coarse mesh (W/m) | Error (%) | qr, refined mesh (W/m) | Error (%) | qr, coarse mesh (W/m) | Error (%) |
| 0.0125 | 708.65 | 4.19 | 680.25 | 0.02 | 681.95 | 0.24 |
| 0.0175 | 694.48 | 2.05 | 680.25 | 0.05 | 681.96 | 0.24 |
| 0.0225 | 688.81 | 1.25 | 680.26 | 0.00 | 681.95 | 0.24 |
| 0.0275 | 685.97 | 0.83 | 680.28 | 0.01 | 681.96 | 0.24 |
| 0.0325 | 684.35 | 0.60 | 680.29 | 0.00 | 681.96 | 0.24 |
| 0.0375 | 683.34 | 0.45 | 680.33 | 0.00 | 681.95 | 0.24 |
| 0.0425 | 682.67 | 0.35 | 680.36 | 0.01 | 681.95 | 0.24 |
| 0.0475 | 682.19 | 0.28 | 680.37 | 0.01 | 681.96 | 0.24 |
