VVT24 - 1D transient solid-liquid phase change (Stefan problem)
| Test case |
|---|
| SVTEST226 |
Description
The purpose of this test case is to determine the one-dimensional temperature distribution along the length of a semi-infinite solid, with the material that is undergoing a phase change, due to an imposed constant temperature load on one end. The imposed temperature is higher than the melting temperature and the initial solid temperature. The model is a one-dimensional problem, thus a single element row can be used to model the semi-infinite solid.
Geometry
A solid geometry part is created by extruding a 10 mm by 20 mm cross-section of a length of 2000 mm.
Simulation model
This model uses the Advanced Thermal solution type.
A 2D mesh of quadrilateral thin shell elements is generated using a 5 mm element size.
The following material properties are used:
- Mass density: ρ = 1 kg/m3
- Thermal conductivity: k = 1.0 W/m·K
- Specific heat at constant pressure: Cp = 10 J/kg·K
- Latent heat: L = 250 J/kg
- Phase change temperature: 0 °C
- Specific heat above phase change: 10 J/kg·K
The following boundary conditions are applied:
- Initial Conditions constraint: Initial Temperature along the face of the geometry with a value of Ti = -2 °C.
- Temperature constraint on the left edge of the face with a value of Ts = -2 °C.
- Temperature constraint on the right edge of the face with a temperature of Tw = 10 °C.
The following solution options are set:
- Solution Type = Transient (the model is simulated for 1 seconds, with 100 time steps and 25 results samples)
The default solver parameters are selected.
Theory
The transient phase change of a one-dimensional problem between solid and liquid phases (due to applied heat or temperature) is known as the one-dimensional Stefan Problem [56] to model ice formation or ice melting. Consider a half-space domain, for example, a one-dimensional material of infinite length in one direction, x∊[0,∞), a material with constant properties undergoing phase change due to an imposed temperature Tw such that it is higher than the melting temperature, and the initial solid temperature, Tw>TM>Ts.
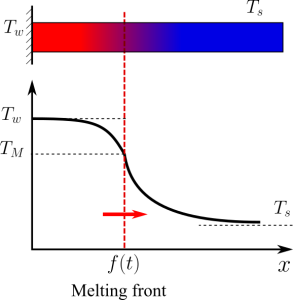
The interface between the liquid and solid, called melting front, moves over time as more solid material changes into liquid. Assuming that liquid and solid phases have the same properties constant density ρ, specific heat cp, and thermal conductivity k, the governing equation for temperature T(x,t) on both solid and liquid parts is:
where D=k/ρcp is the thermal diffusivity.
For this one-dimensional phase-change problem, one can assume different D values for liquid, Dl, and solid, Ds, phases. The relation between the liquid and solid phase is:
where L is the latent heat of melting.
The interface between the liquid and solid phases is a partially melted material [57]. Based on microscopic studies, the thickness is inversely proportional to the temperature gradient in the solid region and is usually very small.
Neglecting the thickness of the interface region, the solution to this problem as a function of time and space [58] is:
For liquid region, x<f(t)
For solid region, x>f(t)
is the obtained by solving the following implicit equation:
where:
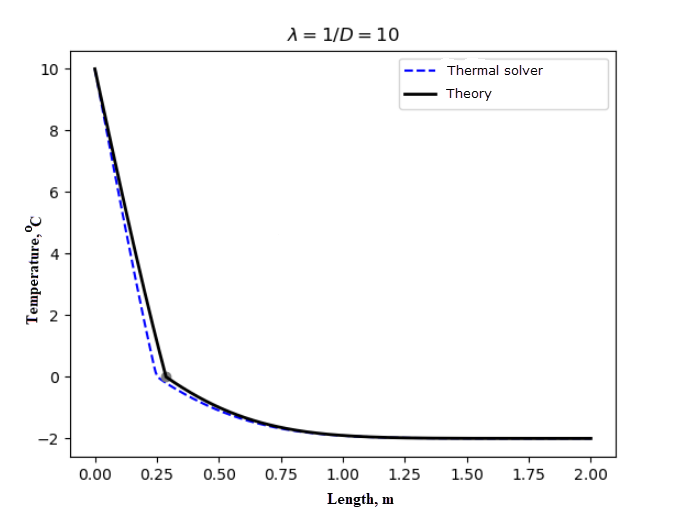
Results
The following figure shows the comparison of the thermal solver results with the theoretical results. The small discrepancy between the theoretical and numerical results can be related to the fact that the model is not an actual infinite 1D model, but a model with a fixed length. As expected, the propagation of melting front in a finite material is slightly higher than in an infinite material of the same property.