VVT23 - Radiation request using Monte Carlo and Deterministic methods
| Solution | Test case | ||
|---|---|---|---|
| Finite volume method | Deterministic | SVTEST224 | |
| Monte Carlo | SVTEST225 | ||
| Finite element method | Deterministic | SVTEST254 | |
| Monte Carlo | SVTEST255 | ||
Description
The purpose of this test case is to compare two computation methods when solving a radiation request model: the statistical Monte Carlo and the analytical deterministic view factor method, which uses the exact calculation. The nodal temperature and view factor results computed by the thermal solver are compared.
Geometry
The geometry consists of a shell block with an immersed cube. The block is partitioned in two volumes with a thin shell surface. The shell block is 250 mm in length, 150 mm in width, 150 mm in height, and has a thickness of 3 mm. The thin shell surface has 1 mm in thickness and located on the distance of 100 mm from the YZ plane along the length. The immersed cube is 50 mm in length with the center located at X=205 mm, Y=105 mm, and Z=105 mm.
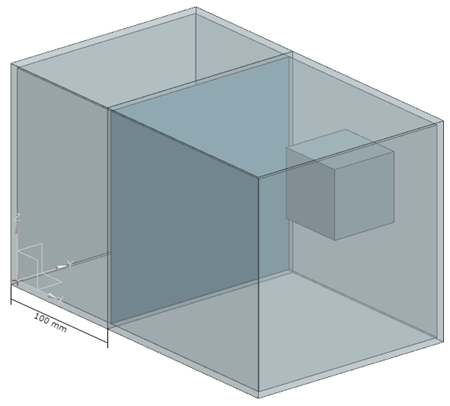
Simulation model
This model uses the Advanced Thermal solution type.
The block, including the inner and outer shell, and the middle surface are meshed with a 2D triangular mesh with a 20 mm element size. The immersed cube is meshed with 2D triangular elements of 15 mm size using the subdivision method.
The following material properties are used:
- Mass density: ρ = 1 kg/m3
- Thermal conductivity: k = 10 W/m·K
The emissivity of the inner shell block, shell cube block and the middle surface faced to the cube is equal to 1. The surfaces radiate from the top. The emissivity of the middle surface that is not faced the cube is equal to 0.5 and radiates from the bottom.
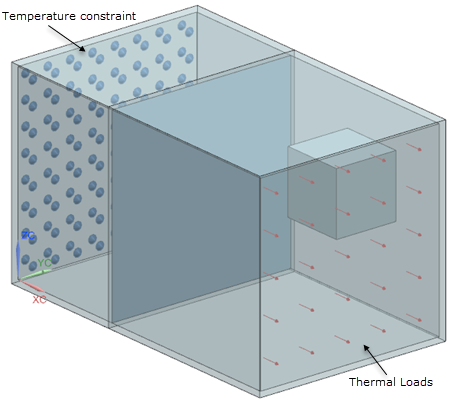
The following boundary conditions are applied:
- Thermal Loads on the internal face of the block with a heat load of 10 W.
- Temperature constraint on the opposite internal face of the block with a temperature of 25 °C.
- Radiation on the 17 internal walls, including the internal block faces, middle surface and the external faces of the cube. For the Monte Carlo method, select the Monte Carlo calculation method and create Monte Carlo Settings modeling object with the Calculate View Factors only check box selected. For the deterministic method, select the Deterministic calculation method.
The default solver options are selected.
Theory
The Monte Carlo method computes radiative exchange by launching rays from defined solar and IR spectrum sources and tracing the rays to extinction, taking into account absorption, reflection (both diffuse and specular), and transmission. It calculates view factors by assembling data from the intersection of rays and elements. This method uses statistical sampling to evaluate the radiative exchange in an enclosure.
Results
The following table compares the average temperatures of the 6 inner faces of the block using the Monte Carlo and Deterministic methods and analytical deterministic methods.
| Face | Tavr (°C), Monte Carlo FVM | Tavr (°C), deterministic FVM | Error (%), FVM | Tavr (°C), Monte Carlo FEM | Tavr (°C), deterministic EM | Error (%), FEM |
|---|---|---|---|---|---|---|
| YZ at X=0 mm | 25 | 25 | 0 | 25 | 25 | 0 |
| YZ at X=250 mm | 105.222 | 107.857 | 2.44 | 105.112 | 107.705 | 2.408 |
| ZX at Y=0 mm | 67.3885 | 68.4732 | 1.58 | 65.995 | 66.994 | 1.491 |
| ZX at Y=150 mm | 67.4042 | 68.4706 | 1.56 | 66.022 | 66.992 | 1.448 |
| YX at Z=0 mm | 67.3971 | 68.4731 | 1.57 | 66.019 | 66.993 | 1.454 |
| YX at Z=150 mm | 68.3982 | 68.4706 | 0.11 | 66.015 | 66.992 | 1.459 |
The following table compares the minimum, maximum, and average view factors sum for the Monte Carlo and deterministic methods. The results are similar with finite volume and finite element methods.
| View factor sum | Monte Carlo | Deterministic | Error, % |
|---|---|---|---|
| Minimum | 0.993665 | 0.998014 | 0.44 |
| Maximum | 1.10793 | 1.00086 | 10.698 |
| Average | 1.05713 | 0.999951 | 5.72 |
