VVT29 - Heat transfer through insulated wall
| Solution | Test case |
|---|---|
| Finite element method in serial | SVTEST262 |
| Finite element method in parallel | SVTEST268 |
Description
The purpose of this validation test is to determine the heat flux and inner (Ti), outer (To) and interface (Tin) solid temperatures of a furnace wall that consist of a steel and insulated brick. The convection to environment boundary condition is applied to the inner and outer faces of the furnace. The steady-state temperatures predicted by the solver are compared with the analytical solutions.
Geometry
The model geometry consists of two 3D plates connected with the area of A = 1000 mm x1000 mm and with the following thicknesses:
- The insulated brick plate (1) of L2 = 100 mm.
- The steel plate (2) of L1 = 5 mm.
Simulation model
This model uses the Multiphysics Thermal solution type.
The plates are meshed with 3D linear hexahedron elements with the size of 50 mm using 3D Swept Mesh.
The meshed elements have the following material and physical properties:
- Plate (1)
- Material: Brick
- Thermal conductivity: k2 = 2.5 W/m·K
- Plate (2)
- Material: Steel
- Thermal conductivity: k1 = 40 W/m·K
The following boundary conditions are applied:
- Convection to Environment constraint on the inner surface of the steel plate with a heat transfer coefficient hi = 200 W/m2◦C and a temperature inside the furnace T f = 900 K.
- Convection to Environment constraint on the outer of the brick plate with a heat transfer coefficient ho = 30 W/m2◦C and a surrounding environment temperature T a = 293.15 K.
The following solution options are set:
- Solution Type = Steady State.
The default solver parameters are selected.
For parallel solve, the Run Solution in Parallel check box is selected. The parallel configuration file is created as follows:
- Solvers selected
- No. processes for Solvers = 4
Theory
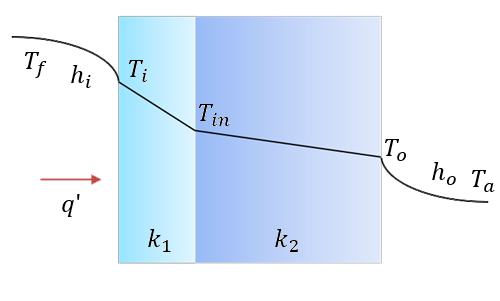
One-dimensional, steady-state heat flow through two plates in series, that are exposed to convection on both sides, is expressed as:
The rate of heat transfer between two plates is equal to the temperature difference divided by the total thermal resistance:
The thermal conduction and convection resistances in the thermal circuit can be determined as follows:
The thermal resistances are in series and the total thermal resistance of the network is:
The heat rate is:
From the steady-state heat flow through two plates in series equation, the inner, outer and interface temperatures are:
Results
The following table compares the average nodal temperature results, predicted by the thermal solver using finite element method, with the calculated theoretical results. The numerical results for heat flux are the same as the theoretical solution for the first two decimal digits.
| Parameter | Theory | Serial Solve | Parallel Solve |
|---|---|---|---|
| q'(W) | 7734.679 | 7735 | 7735 |
| To(K) | 550.97 | 550.97 | 550.97 |
| Tin(K) | 860.36 | 860.36 | 860.36 |
| Ti(K) | 861.33 | 861.33 | 861.33 |
