VVT11 - Two-dimensional heat transfer with convection
| Solution | Mesh | Test case | |
|---|---|---|---|
| Finite volume method | Coarse | SVTEST14 | |
| Fine | SVTEST15 | ||
| Finite element method | Coarse | SVTEST240 | |
| Fine | SVTEST241 | ||
Description
The purpose of this test case is to determine the temperature at a specific point on a plate. The plate has 4 edges: one edge has fixed temperature, second edge has insulation and two others edges have convection to the environment.
Geometry
The plate is created by extruding a rectangular section, 0.6 m wide by 1 m height, to an arbitrary thickness. The right-hand face of the plate extrusion is split a distance of 0.2 m from the bottom edge.
Simulation model
The first 2D mesh is made of quadrilateral thin shell elements. An element size is 200 mm. The second refined mesh is created close to the point where the temperature measurement takes place. The two edges resulting from the split face operation are assigned mesh controls that biased the mesh density towards the point (0.6 m, 0.2 m).This is shown in the following figures.
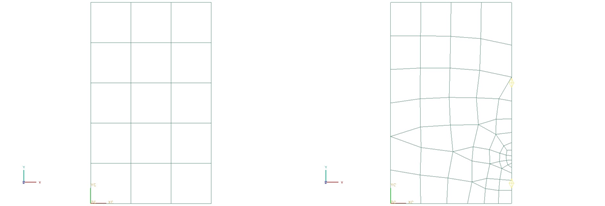
The meshed elements have the following material and physical properties:
- Thermal conductivity: k = 52.0 W/m·°C.
- Thickness: arbitrary
- Mass density: arbitrary
The following boundary conditions are applied:
- Temperature constraint on the bottom edge of the plate with a value of Tb= 100 °C.
- Convection to Environment constraint on the right-hand and top edges of the plate with a heat transfer coefficient h = 750 W/m2°C and a surrounding environment temperature T = 0 °C.

The following solution options are set:
- Solution Type= Steady State
All other attributes are left at the defaults.
The default solver parameters are selected.
Theory
Two-dimensional steady-state heat flow in a plate with no heat generation is governed by the heat equation:
For this case, the boundary conditions are defines as:
The solution to this partial differential equation is given in [3]:
where
, and
are the roots of
.
At coordinates (0.6 m, 0.2 m), the analytical solution for the temperature is 18.3 °C.
Results
As shown in the table, refining the mesh in the vicinity of point (0.6 m, 0.2 m) improved the accuracy of the solution.
| Finite volume method | Finite element method | |||||
|---|---|---|---|---|---|---|
| Ttheory (ºC) | Tcoarse mesh (ºC) | Error (%) | Trefined mesh (ºC) | Error (%) | Trefined mesh (ºC) | Error (%) |
| 18.3 | 20.3 | 10.9 | 18.1 | 1.1 | 17.99 | 1.72 |
