VVT32 - Radiation heat transfer in a conical furnace
| Test case |
|---|
| SVTEST266 |
Description
The purpose of this case is to model a furnace that has the form of a truncated cone and determine the temperature of the lateral wall.
Geometry
The furnace is modeled as a solid truncated cone with the two circular bases. The top diameter (D1) of the cone is 600 mm, the bottom diameter (D2) is 1200 mm, and the cone height (H) is 1200 mm.
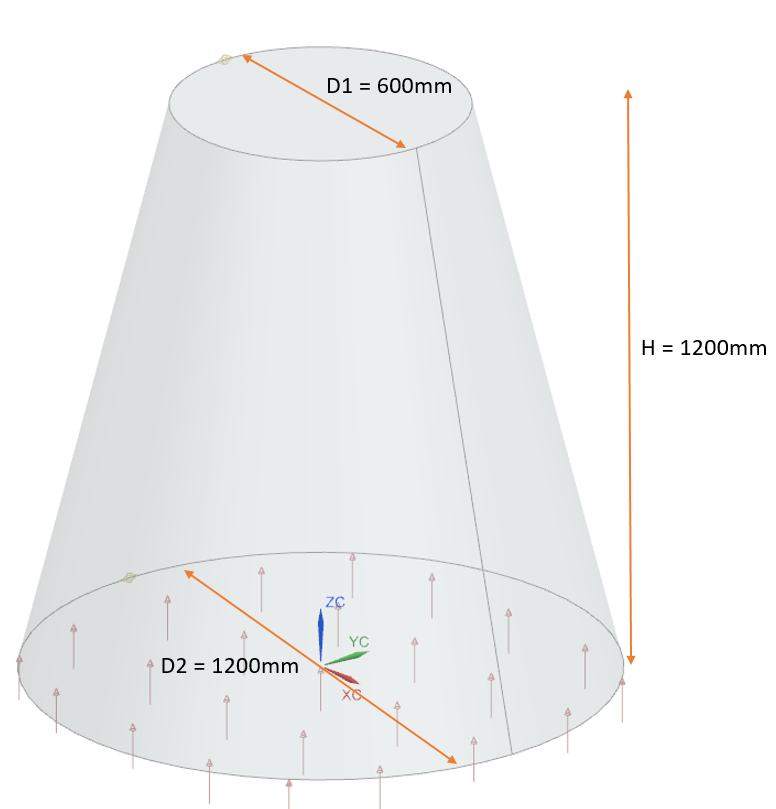
Simulation model
This model uses the Thermal solution type.
The top and the bottom cone surfaces are meshed with a 2D triangular null shell elements with an element size of 100 mm. The lateral cone surface is meshed with a quadrilateral null shell mesh with an element size of 100 mm.
The following thermo-optical properties of the elements were defined:
- Top surface emissivity: ε1 = 0.70
- Bottom surface emissivity: ε2 = 0.40
- Lateral surface emissivity: ε3 = 1
All surfaces radiate from the bottom.
The mesh has no material or physical properties assigned to it.
The following boundary conditions are applied:
- Temperature constraint on the top surface mesh with a value of T = 500 K.
- Temperature constraint on the bottom surface mesh with a value of T = 650 K.
- Thermal Loads: Heat Load on the bottom surface mesh with a value of q = 1400 W.
The following solution options are set:
- Solution Type = Steady State
This model is computed using a graphics processing unit (GPU) with an NVIDIA Quadro P2000 graphics card.
The default solver parameters are selected.
Theory
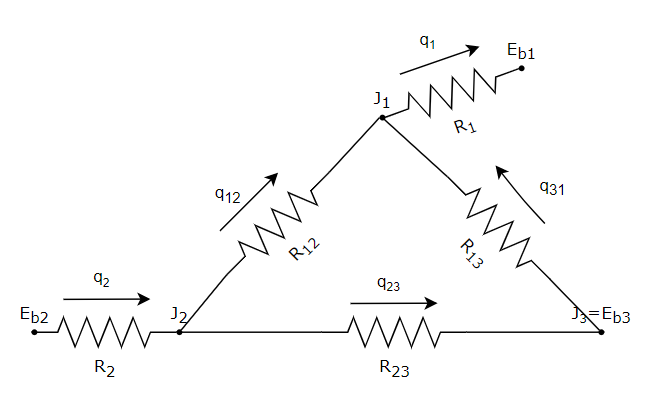
The following thermal circuit diagram shows the radiation heat transfer of three surfaces: top surface (1), bottom surface (2) and lateral surface (3).
For parallel coaxial disks of unequal radius, the shape factor is computed as follows:
With:
Where i and j are indices designating the coaxial disks, r is the radius of the disk and H is the cone height.
The shape factor from the lateral surface (3) to the base surface (i=1,2):
With:
Where i,j = 1,2 and i≠j.
Since the top and bottom surfaces are flat, F11 = F22 = 0, and based on the enclosure identity:
The radiative resistances can be determined as follows:
Using the Stephan-Boltzmann law, the radiosity on bottom surface can be computed:
The energy balance can be written as:
The radiosity on lateral surface is then:
With:
The temperature on the lateral surface can be calculated with the Stephan-Boltzmann law:
Results
The model solved in 17 seconds with a GPU on 1 core.
The following table compares the average nodal temperature results at the lateral surface, predicted by the thermal solver, with the calculated theoretical results. The simulation results are in agreement with the theoretical values.
| Parameter | Theory | Simulation - Average | Error (%) |
|---|---|---|---|
| T3 (K) | 604.12 | 612.42 | 1.33% |
