VVT27 - Concentric spheres with uniform temperatures
| Test case |
|---|
| SVTEST259 |
Description
The purpose of this validation test is to determine the temperatures of multiple enclosures with uniform temperatures.
Geometry
The model geometry consists of the three concentric spheres with the radiuses: r1 = 5 mm, r2 = 50 mm, r3 = 100 mm.
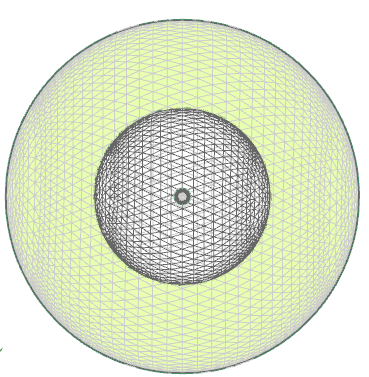
Simulation model
This model uses the Thermal solution type.
The small, middle, and big surfaces are meshed with 2D triangular null shell elements with an element size of 1, 5, 7 mm, respectively.
The mesh has no material or physical properties assigned to it.
Temperature constraint is applied on the small sphere surface mesh with a value of T = 200 °C.
The following solution options are set:
- Solution Type = Steady State
- Radiative Environment Temperature = -273.15 °C.
This model is computed using the graphics processing unit (GPU) with NVIDIA Quadro P2000 graphics card.
The default solver parameters are selected.
Theory
The following thermal diagram models radiation heat transfer between the small, middle, and big surfaces.

The view factors between the spheres are:
The radiation heat transfer is constant and can be determined between the small sphere and the environment as follow:
The radiative resistances can be determined as follows:
The equivalent resistance of the network is:
From the heat transfer equation, the radiosity J2 is:
From the Stephan-Boltzmann law, the temperature of the middle sphere surface is:
Using a similar approach, you can calculate the radiosity J3 and temperature T3 of the big sphere as:
Results
The model solves in 3 min 58 sec with a GPU on 1 core.
The following table compares the temperature and radiosity results predicted by the thermal solver with the calculated theoretical results, at the middle and big sphere's surfaces.
| Parameter | Theory | Simulation | Error (%) |
|---|---|---|---|
| J2(W/m2) | 35.08 | 34.78 | 0.9 |
| J3(W/m2) | 7.017 | 6.948 | 1 |
| T2(°C) | -115.433 | -115.769 | 0.2 |
| T3(°C) | -167.679 | -167.933 | 0.2 |
The discrepancies mostly come from the model's geometry. Meshing spherical surfaces with linear elements represents an approximation of the curvature, which leads to the discrepancy between the theoretical and computed results.
You can also estimate the error in the radiosity using the Stephan-Boltzmann law:
Neglecting higher order terms:
And hence:
Therefore, the radiosity error is expected to be about 4 times higher than the temperature error.
