VVT16 - Thermal void on an edge of a rotating component
| Solution | Test case |
|---|---|
| Finite volume method | SVTEST21 |
| Finite element method | SVTEST247 |
Description
This validation case examines the thermal void boundary condition applied to the edge of a two-dimensional axisymmetric rotating model. The steady-state temperature results predicted by the solver are compared to the analytical solution.
Geometry
The model geometry consists of an aluminum pipe with the length of 200 mm, inner radius of 20 mm, and outer radius of 120 mm.
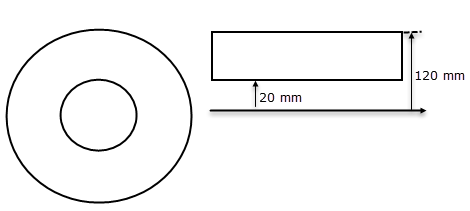
Simulation model
This model uses the Simcenter Multiphysics solver.
2D mesh is generated using axisymmetric linear quadrilateral elements with the size of 10 mm.
The meshed elements have the following material and physical properties:
- Material: Aluminum
- Mass density: ρ = 2660 kg/m3
- Thermal conductivity: k = 117 W/m °C
- Specific heat at constant pressure: Cp = 900 J/kg °C
The following boundary conditions are applied:
- Thermal Void on the edge at the radius of 120 mm with a heat load Q = 100 W, a heat transfer coefficient h = 0.01 W/mm2·°C and a swirl velocity vφ =100 mm/s (Rotational effects is set to Relative Temperature Reference Frame.)
- Temperature constraint on the surface at the radius of 20 mm with a value of T = 60 °C.
- Rotation load on the whole model with angular velocity ω =1000 rad/s.
The default solver parameters are selected.
Theory
Two-dimensional steady-state heat flow in a cylindrical coordinate system with no heat generation and with the heat conduction in one direction is governed by the heat equation [1]:
The solution to this differential equation is given by:
The coefficient C2 at r=r1 is obtained as follows:
where T1 is the temperature on the surface at r1.
The coefficient C1 at r=r1, where the conduction into the outer edge equal the convection from the outer edge, is obtained as follows:
The solution to this differential equation is defined as:
where:
- T2 is a temperature on the surface at r2.
- Tf is a void fluid temperature.
Replacing the coefficients C1 and C2 in the solution to the differential equation, gives the metal temperature,T2 , on the surface at r2:
The void fluid temperature is defined by solving the energy equation for a thermal void. The thermal void represents a volume of a fluid at a constant equilibrium temperature at any time, that convects with surrounding metal. The energy equation is given by:
where:
- j =1, 2, …,N represents the metal elements surfaces in contact with the void fluid at its boundaries.
- Ts,j is the metal element edge temperature.
- hj is the specified local heat transfer coefficient.
- Aj is the solid-fluid interface area.
- Q is the power input into the void.
- ρ is the density of the fluid material in the void cavity.
- V is the volume of the void cavity.
- Cp is the specific heat of the fluid material in the void cavity.
Capacitance can be set to finite, however, typically, it is defined as having zero capacitance:
For the rotating components that surround the fluid, the specified fluid temperature is assumed to be the relative void temperature, Tf=Tv,rel and Ts,,j=T2. The energy above can be rewritten as:
where A=2πrL.
Solving energy equation and the equation above gives the analytical solution for the void metal temperature, T2, and relative void temperature Tv,rel.
The total absolute temperature can be calculated by solving following equation:
where the relative temperature difference is given by the following equation, assuming constant specific heat, Cp, and an ideal gas:
where:
- ω is the angular velocity.
- vφ is the fluid swirl velocity.
- vax is the fluid axial velocity.
Results
The following table compares the void metal temperature and the total absolute temperature computed by the thermal solver with the analytical solution.
| Finite volume method | Finite element method | ||||
|---|---|---|---|---|---|
| Parameter | Ttheory (°C) | Tsim (°C) | Error (%) | Tsim (°C) | Error (%) |
| T2 | 61.21 | 61.22 | 0.016 | 61.215 | 0.0082 |
| Tv,rel | 61.276 | 61.29 | 0.0067 | 61.281 | 0.0082 |
| TT,abs | 54.01 | 54.16 | 0.27 | 54.155 | 0.2685 |
