VVF3 - Unsteady incompressible laminar Couette flow
| Test case |
|---|
| SVTEST124 |
Description
This test case examines the unsteady incompressible laminar Couette flow between two infinite flat plates, where one of the plates is instantly accelerated from rest to U0. The velocity profiles are compared to theoretical results.
Geometry
The geometry is a rectangular cube, 10 mm in length.
Simulation model
The swept mesh is made of hexahedral elements. The following mesh controls are used:
- Height: 20 elements
- Width: 2 elements
- Length: 20 elements
The following figure shows the generated mesh.

The fluid is modeled using incompressible air with the following properties:
- Mass density: ρ = 1.207 kg/m3
- Dynamic viscosity: µ = 1.85e-005 Pa·s
- Specific heat at constant pressure: Cp = 1007 J/kg·K
The gas constant is kept blank in order to simulate a truly incompressible flow.
The following boundary conditions are used:
- Periodic Boundary Condition on the front and back surfaces.
- Flow Surface: Boundary Flow Surface on the top surface using the No Slip Wall option with smooth wall friction.
- Flow Surface: Boundary Flow Surface on the bottom surface with:
- Wall Treatment set to the No Slip Wall option with smooth wall friction.
- The Rotating/Translating Surface in Share option selected and the Translating type of motion specified in the X direction with a velocity of 10 m/s.
- Symmetry Plane on the right and left surfaces.
This model uses Advanced Flow solution type with the following options:
- Turbulence Model: None (Laminar Flow)
- Solution Type: Transient with a time interval going from 0 to 4 seconds
The following solver parameters are selected:
- 3D Flow Solver: Maximum Residuals = 1e-6
- 3D Flow Solver: Momentum advection scheme: SOU with automatic limiter
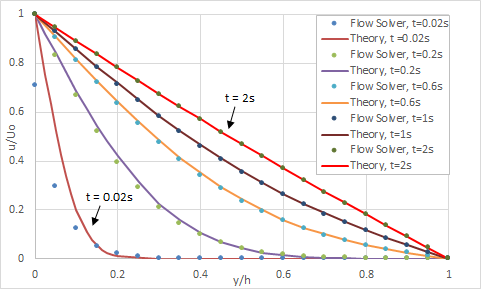
Theory
The theory described by White [8] is used as a basis of comparison for the solver results. The velocity profiles are computed as:
where:
- u is the flow velocity.
- U0 is the bottom plate velocity.
- h is the spacing between the two plates.
- t* is equal to vt/h2.
- v is the kinematic viscosity.
Results
The velocity profiles in function of time are presented in the following figure.