VVF22 - Bursting membrane boundary condition
| Test case |
|---|
| SVTEST214 |
Description
This validation case examines the bursting membrane boundary condition, which represents a disposable wall that bursts under certain conditions. After the membrane bursts, it acts as an open window connecting the flow regions that straddle the membrane.
Geometry
The geometry consists of two boxes: inner 50x50x50 mm3 box and outer 100x100x100 mm3 box.
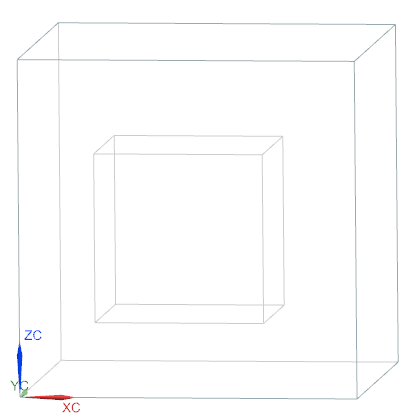
Simulation model
This model uses the Advanced Thermal-Flow solution type.
The fluid domain in both boxes is meshed using 3D tetrahedral elements. The solid null shell walls of the inner box is meshed using 2D linear triangular shell elements. The element size for both 3D and 2D meshes is 10 mm. Mesh matting is applied to the walls of the inner box.
The fluid is modeled using air with the following properties:
- Mass density: ρ = 1.207 kg/m3
- Thermal conductivity: k = 0.0263 W/m·C
- Dynamic viscosity: µ = 1.85e-005 Pa·s
- Specific heat at constant pressure: Cp = 1007 J/kg·K
- Gas constant: R = 287 J/kg·K
The following boundary conditions are applied:
- Flow Boundary Condition: Bursting Membrane on the XZ face of the inner box with a pressure differenceof 500 kPa.
- Flow Boundary Condition: Opening on the YX face of the outer box.
- Flow Surface: Embedded Flow Surface on the walls of the inner box, where the convection properties option is set to No Convection-Adiabatic.
-
Heat Load on the inner box with a heat load value of 5000 W.
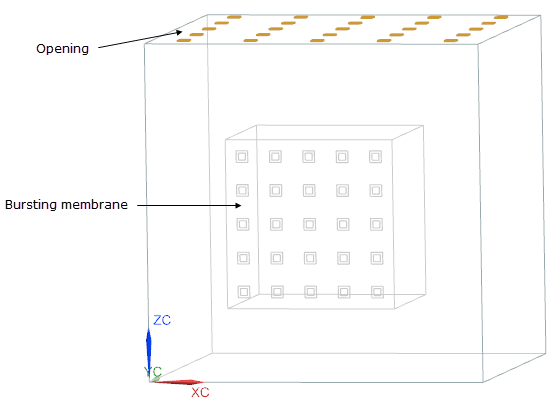
The following solution options are set:
- Turbulence Model:Mixing Length
- Buoyancy: Selected
- Solution Type: Transient
-
3D Flow: Default Convection Properties is set to No Convection - Adiabatic
-
Transient Setup: End Time = 0.05 s, Thermal Time Step Option = 0.0005 s
The default solver parameters are selected.
Theory
The behavior of the ideal gas can be described by the following universal equation of state:
where:
- P is the gas absolute pressure.
-
n is the number of moles of gas.
- T is the absolute temperature.
- V is the volume.
- R is the universal gas constant equal to 8.31 J/mol·K.
The process described in this validation case is isochoric, in which the volume of the closed system remains constant. It describes the behavior of the gas inside the container that cannot be deformed.
The isochoric process is expressed with the ideal gas law as:
Results
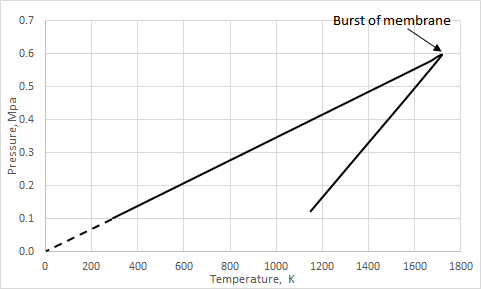
In a closed enclosure, where the volume and amount of air are constant, the pressure and temperature are directly proportional until the state of the relevant membrane is switched to open. If the temperature on the kelvin scale increases by a certain factor, the gas pressure increases by the same factor, as shown in the graph.