VVF10 - Oxygen-nitrogen gas mixture
| Geometry | Test case |
|---|---|
| Case1 | SVTEST174 |
| Case2 | SVTEST175 |
| Case3 | SVTEST176 |
| Case4 | SVTEST177 |
| Case5 | SVTEST178 |
| Case6 | SVTEST179 |
Description
This test case examines the oxygen-nitrogen O2 − N2 gas mixture properties for various gas volume fractions at ambient temperature and pressure. The figure below illustrates the initial stage where two gases are completely segregated: the heavy gas O2 occupies the upper part, the light gas N2 occupies the lower part.
Geometry
The geometry is a cube, 100 mm in length, shown in the following figure.
The cube is partitioned along the height, H, to give two sections, corresponding to the volume fraction of two different gases. Six models for different O2 and N2 volume fractions were developed, listed in the following table.
| Case | Volume fraction O2 (%) | Volume fraction N2 (%) | H (mm) |
|---|---|---|---|
| 1 | 13.2 | 86.8 | 86.8 |
| 2 | 25.6 | 74.4 | 74.4 |
| 3 | 41 | 59 | 59 |
| 4 | 51 | 49 | 49 |
| 5 | 66 | 34 | 34 |
| 6 | 76 | 24 | 24 |
Simulation Model
This model uses Advanced Thermal-Flow solution type.
The mesh is made of tetrahedral elements.
The gases are modeled using the oxygen and nitrogen from the default material library properties: mass density, dynamic viscosity, and specific heat vary with temperature.
Oxygen gas, O2:
- Molar mass: 0.032 kg
- Specific gas constant: 259.8 J/kg·K
Nitrogen Gas N2:
- Molar mass: 0.028 kg
- Specific gas constant: 296.8 J/kg·K
The following boundary conditions are applied:
- Initial Conditions constraint: oxygen O2 mass fraction from table above
- Initial Conditions constraint: nitrogen N2 mass fraction from table above
The following solution options are set:
- Turbulence Model:None (Laminar Flow), Buoyancy check box selected
- Solution Type: Transient (0 to 250 seconds)
- Ambient Conditions: Pressure = 0.101351 N/mm2 (MPa), fluid temperature = 25.02 ºC
The following solver parameters are set:
- 3D Flow Solver: Time Step = 0.1 s
- 3D Flow Solver: Maximum Residuals = 1e-6
- 3D Flow Solver: Buoyancy Model: Full with Hydrostatic Pressure
Theory
The theory described by Poling [17] is used as a basis of comparison between the solver results and the theory. The mixture density is computed as:
where:
- RO2 and RN2 are the specific gas constants of oxygen and nitrogen, respectively.
- T is the gas mixture temperature.
- PO2 and PN2 are the partial pressure of oxygen and nitrogen, respectively.
The partial pressure exerted by a gas of the mixture is defined as:
where:
- Nn is the number of moles of a gas in the mixture.
- R is the universal gas constant.
- V is the volume of the mixture equal to 0.001 m2.
Mass fraction of nitrogen in the mixture is calculated as follows:
where:
- XN2 and XO2 are the volume fractions of nitrogen and oxygen, respectively
- ρN2 and ρO2 are the densities of nitrogen and oxygen, respectively.
Results
The mixture density as a function of percentage of nitrogen and oxygen is presented in the following figure.
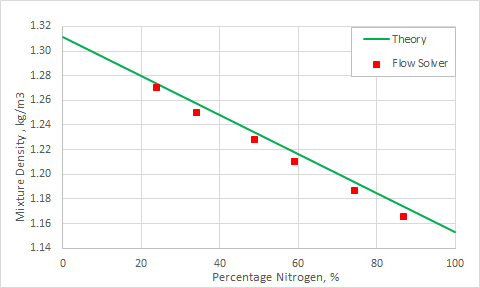
Computed mass fractions for nitrogen N2 are compared with the theoretical values in the following table. All the errors are under 0.5%.
| Case | Mass fraction N2 (%) | Error (%) | |
|---|---|---|---|
| Theory | Flow solver | ||
| 1 | 85.3 | 85.7 | 0.51 |
| 2 | 71.9 | 72.1 | 0.3 |
| 3 | 55.9 | 55.8 | 0.06 |
| 4 | 45.8 | 45.7 | 0.23 |
| 5 | 31.2 | 31.1 | 0.04 |
| 6 | 21.7 | 21.6 | 0.19 |
