Understanding the preconditioned conjugate gradient solver and convergence checks in temperature calculation
This article explains the preconditioned conjugate gradient solver, which is used by the thermal solver, preconditioning techniques, convergence criteria, and memory management strategies to enhance convergence speed and numerical stability of your thermal simulations.
Preconditioned conjugate gradient solver
- Initialization—The solver assigns initial values to element temperatures, conductances, and heat inputs.
- Defining the system of equations—The solver defines the system of equations that describe the thermal model and calculates parameters such as total pressures for hydraulic elements and both linear table interpolations and table-dependent conductances.
- Computing temperatures—The preconditioned conjugate gradient solver computes temperatures using the bi-conjugate gradient method with a Newton-Raphson scheme for non-linear terms.
- Verifying convergence—The solver checks if the solution meets the convergence criteria.
- Incrementing the time—The solver increments the time and updates the system of equations for the next time increment.
- Writing results—The solver writes the temperature and other requested results to the results file, which Simcenter 3D reads.
The preconditioned conjugate gradient solver is an iterative method for solving large, sparse systems of linear equations. It is an enhancement of the standard conjugate gradient (CG) method, designed to improve convergence speed and numerical stability.
- Conjugate gradient method
- Uses the bi-conjugate gradient stabilized technique to solve for
temperatures. The equations are placed into the matrix format:where:
- is the conductance matrix.
- is the temperature vector estimate at the n+1 iteration of the conjugate gradiaent solver at the time step t+dt, without any damping applied. This vector represents the approximate temperatures at different nodes or points in the domain during the iterative process of solving the system of equations.
- is the right-hand side vector.
- Preconditioning
- Uses an approximate inverse matrix as a preconditioner to accelerate convergence. The preconditioning matrix is created using the incomplete lower-upper (ILU) factorization method. The preconditioning matrix is updated every ten iterations for steady-state runs or integration time steps for transient runs. Additionally, before every solution, the solver checks the diagonal terms of the [GG] matrix for any changes since the last update of the preconditioning matrix. If the change exceeds 100%, the preconditioning matrix is automatically updated.
Convergence criteria and memory allocation for conjugate gradient solvers
The preconditioned conjugate gradient solver converges when the residual value is less than the convergence criterion. This is monitored and displayed with the following message:
ILU iteration 1 Residual= 1.76E-02
ILU iteration 2 Residual= 3.96E-03
ILU iteration 3 Residual= 4.64E-04
ILU iteration 4 Residual= 1.82E-04
ILU iteration 5 Residual= 8.75E-05
ILU iteration 6 Residual= 4.04E-05
ILU iteration 7 Residual= 2.05E-05
ILU iteration 8 Residual= 1.22E-05
ILU iteration 9 Residual= 8.32E-06
ILU iteration 10 Residual= 5.56E-06
4952
** Conjugate-gradient solver did not converge in 100 iterations.
** Solution automatically restarting with matrix fill value 210.
** Information: Residual= 6.070E-06, Target = 1.000E-05, Matrix fill = 200
** No user intervention required.- If the convergence pattern is promising, it increases the maximum number of allowable iterations to 200, 300, etc.
- If the convergence pattern is not promising, it increases the preconditioner matrix fill value in increments of 10, up to a maximum value of 200. The preconditioning matrix is then re-created until convergence is achieved.
You can specify a higher value in the Preconditioner Matrix Fill Value box for ill-conditioned matrices. It increases the convergence, however requires more CPU time.
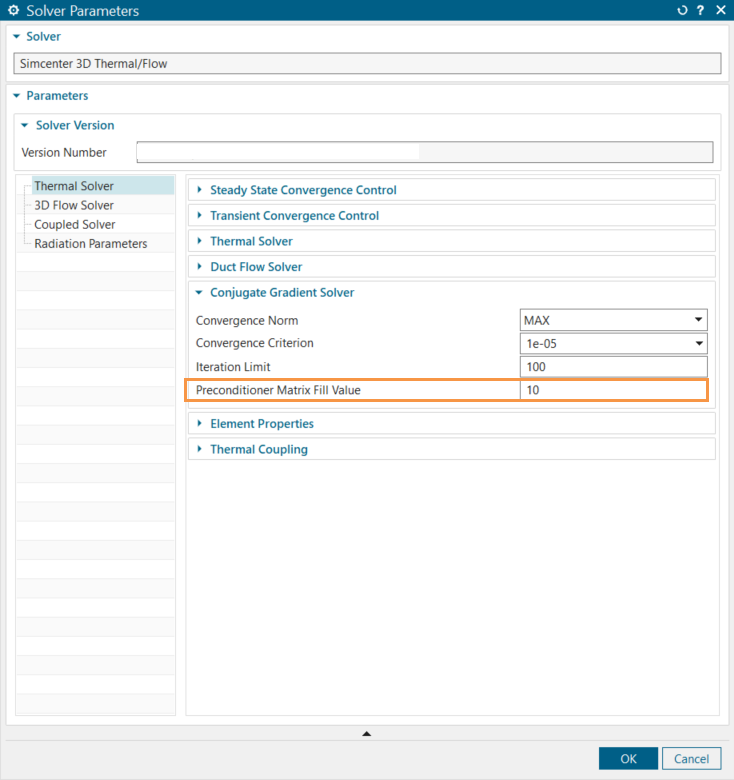
When convergence is difficult, this may lead to a large system to solve and large memory consumption. Verify if you have the following message in the <simulation/model name>-<solution/analysis name>_verbose.log file, the old MSGF file:
7951
** Unable to allocate sufficient memory to solve the model with a
** matrix fill value of 70. Trying to allocate 42957668352. bytes,
** 11222808612 have already been allocated. Possible cause: insufficient
** swap space. Suggestion: if you find the residual value
** acceptable, increase the convergence criterion to something
** above this value.If the residual value is acceptable, increase the convergence criterion.
You can also modify the type of convergence norm. The Max norm captures only the largest residual, revealing the worst local error regardless of overall behavior. Even a single large deviation will be detected. In contrast, the L2 norm averages residuals across the model, making the impact of largest residuals less pronounced. Therefore, a small Max norm ensures low error everywhere; a small L2 norm ensures only a low average error—big, localized spikes could still exist.
To request the timing and memory information in thermal solver modules, include the INCLUDE TIMING INFO IN VERBOSE OUTPUT and INCLUDE MEMORY INFO IN VERBOSE OUTPUT advanced parameters to your solution.
