How to model a constant conductance heat pipe?

Model description

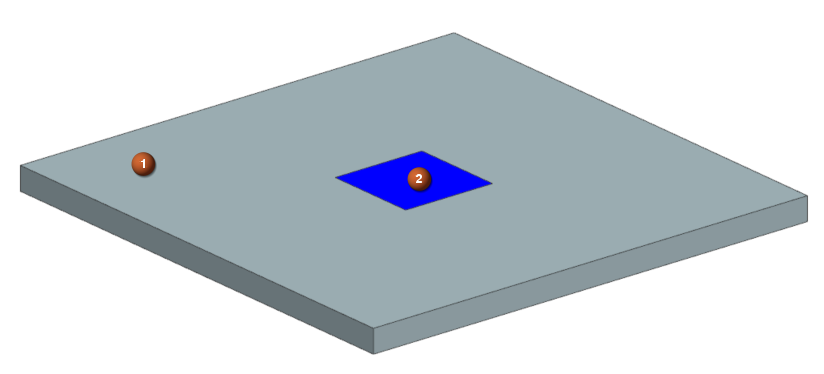
The model consists of a honeycomb panel covered with aluminum outer and inner facesheets. Radiation from the inner facesheet is not included in the model. The honeycomb panel is exposed to deep space. A power supply unit (PSU) is located at the center of the panel and dissipates 125 W.

Geometry and dimensions

Honeycomb panel (1): 0.5 m x 0.5 m
PSU (2): 0.1 m x 0.1 m, placed at the center
Panel facesheets thickness: 0.5 mm

Material properties

Honeycomb core density: 50 kg/m³
Honeycomb core conductivity: 2.8 Wm^-1K^-1
PSU aluminum baseplate (1) thickness: 4.5 mm
Panel aluminum facesheets thickness: 0.5 mm
- Outer facesheet (2): covered with silver teflon with emissivity of 0.07 and absorptivity of 0.78
- Inner facesheet (3): covered with iridite
Aluminum:
- Density: 2780 kg·m³
- Thermal conductivity: 151 m·K^-1
- Specific heat: 87^-15 J·kg^-1·K^-1

Hand calculations show that a 0.5 m x 0.5 m panel with an emissivity of 0.78 dissipating 125 W and viewing only deep space has a temperature of 53 ºC when the heat load is distributed over the entire panel.

Thermal model without a heat pipe

The facesheets are explicitly modeled, while the core is represented by a thermal coupling between them. The PSU base is included by increasing the thickness of the facesheet elements under the unit from 4.5 mm to 5 mm. Thermal resistance between the PSU and the facesheet is ignored, but it is acceptable for this example.

Boundary conditions

Thermal Coupling between facesheets

Primary selection: elements of the outer facesheet
Secondary selection: elements of the inner facesheet
Type: Conductive Gap
Gap Thermal Conductivity: 2.8 W/(m·K)
Coupling Resolution: medium
Only Connect Overlapping Elements check box is selected

Radiation

Type: Enclosure Radiation
Applied to: elements of the outer facesheet
Include Radiative Environment is selected
Calculation method: Hemicube Rendering
View Factor Accuracy: medium
Elements not Part of this Enclosure Can Shadow is cleared

Thermal Load

Type: Heat Load
Applied to: elements of the baseplate
Heat Load: 125 W

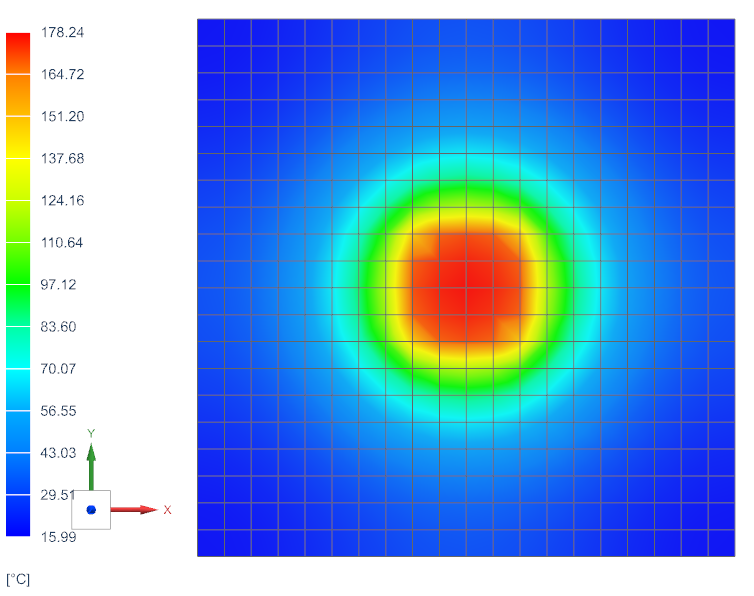
Temperature results

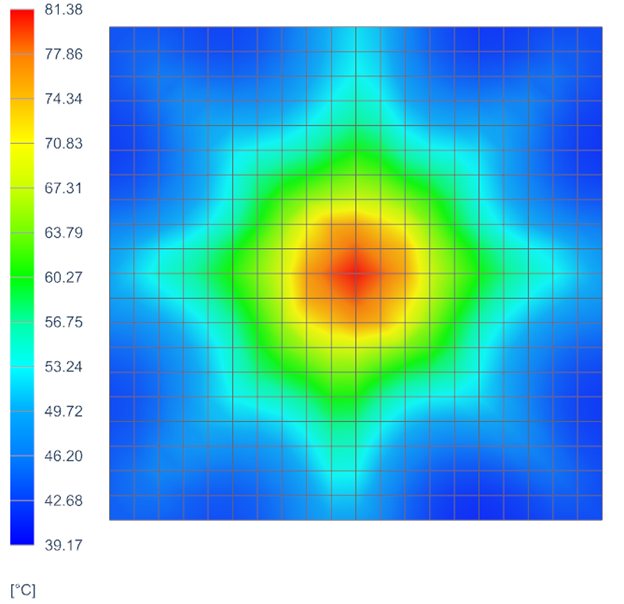
The maximum temperature is 178.24 ºC, which is significantly higher than the 53 ºC predicted when the load is distributed over the entire surface. Heat pipes are very helpful in this situation as they have a high thermal conductivity, which allows them to transfer heat away from the PSU quickly reducing the maximum temperature.

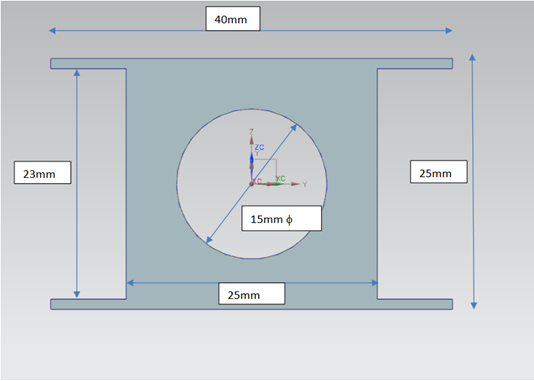
Selecting heat pipes

The core of the panel is 25 mm thick. To embed heat pipes, the selected unit also needs to be 25 mm thick. The following image shows a selected profile. The grooves in the walls of the heat pipe are not shown.

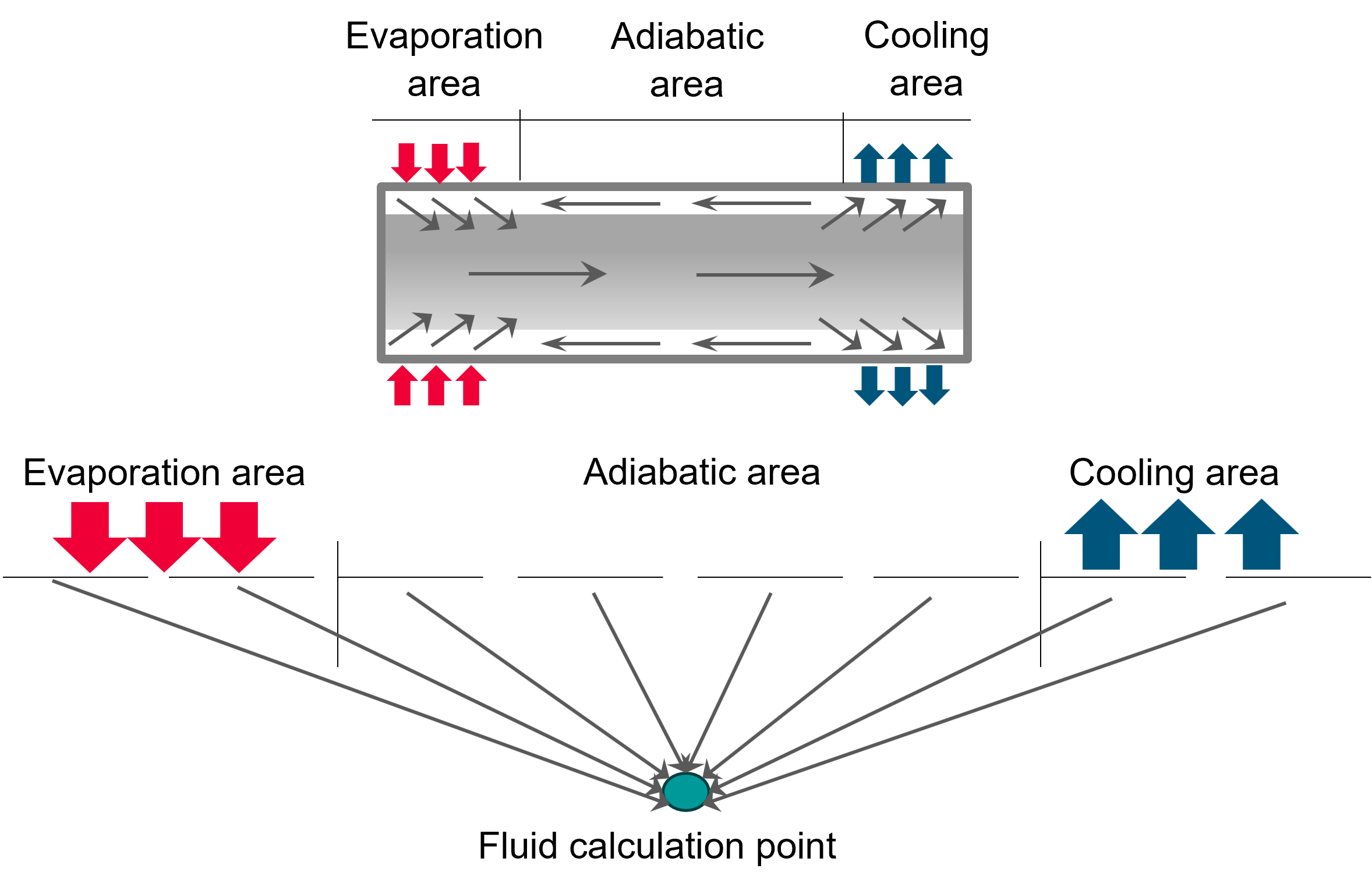
The heat pipe is modeled using beam elements to represent its structure. These beams are connected to the fluid inside the heat pipe using the Thermal Device simulation object with a Heat Pipe type that models the evaporation and condensation heat transfer coefficients and their connection to the fluid. The condensation and evaporation sections are determined based on the relative temperatures of the solid and fluid elements.

The beams representing the structure must be assigned the following properties:


Property	Description	Value
Material	Structure material	Aluminum
Cross section area	Area of heat pipe section	478.3 mm² If mass per unit length is known, cross sectional area can be calculated as (m·L)/ρ
Perimeter	Circumference of fluid channel, non-including fluid grooves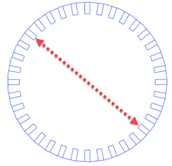	π·15 mm = 47.1 mm

The beams representing the heat pipe structure are connected to the facesheets with a thermal coupling that has a defined conductance per unit length. This value can be estimated through hand calculations or determined from a thermal model of a small section of the heat pipe structure.

Thermal modeling of a heat pipe

A heat pipe is modeled using the following boundary conditions:

A temperature of 0 °C is applied to the top surface.
A temperature of 10 ºC is applied to the core surface.
A 10 ºC temperature difference is used because the model is 0.1 m long; the heat flow from the core to the top would be the same as a 1.0 m long section with a 1 ºC temperature difference.

To review the model heat flows, inspect the <simulation/model name>-<solution/analysis name>.log file. At the end of the file, the summary of heat flows shows a heat flow of 523.8 W between the two temperature sinks. The beam elements are connected to the facesheets with a thermal coupling of 2*523.8 W·m^-1·K^-1, for half the thickness. If different lengths and temperature differences are used for the heat pipe model, the heat flow should be normalized to a 1ºC temperature drop and 1 m length.

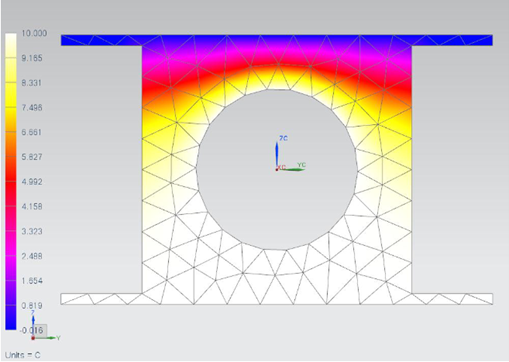
Thermal model with a selected heat pipe

Beam elements are added to the panel to represent the structure of the heat pipe. In this case, a radial grid of heat pipes is selected. The cross-sectional area and perimeter are set as described in the preceding table. The following figure shows the heat pipe elements along with one of the facesheets.

To model the heat pipe fluid, the Thermal Devices simulation object of the Heat Pipe type is used. It automatically creates a fluid node connected to the selected elements. You can define the coupling as a single equivalent heat transfer coefficient for the whole heat pipe or separate values for the condenser and evaporator sections. Alternatively, you can skip modeling the fluid and directly specify the total conductance for the heat pipe. The best approach depends on the information from the heat pipe supplier. The most accurate method is to use separate heat transfer coefficient values. However, these values are often similar or may not be available, and, therefore, an equivalent heat transfer coefficient for both regions is used.

Typical values for axial extrusion heat pipes are 7500 W/m²°C for the condensing region and 5000 W/m²°C for the evaporating region. These values might be higher for sintered wicks. Vendors usually provide the effective conductivity for the whole pipe, which you can use to back-calculate the coefficients if needed.

For this model, the same value is used for both evaporation and condensation. A sensitivity analysis showed that the panel temperature changed very little when this value was halved, so using a single value is a reasonable approach in this case. Note that to obtain separate post-processing data for each heat pipe, one Thermal Devices simulation object is created for each beam section — eight in total.

Boundary conditions

To obtain separate post-processing data for each heat pipe, create a Thermal Devices simulation object for each beam section.

Type: Heat Pipe
Applied to: elements of the beam
Type: Equivalent Heat Transfer Coefficient
Coefficient: 7500W/(m²·°C)

Thermal Coupling for the heat pipe to the outer facesheet

Type: Thermal Coupling
Primary selection: elements of the beams
Secondary selection: outer facesheet
Magnitude type: Edge Contact
Conductance per Length: 2*523.8 W/(m·°C)
Coupling resolution: One-to-One
Only Connect Overlapping Elements check box is cleared

Thermal Coupling for the heat pipe to the inner facesheet

Type: Thermal Coupling
Primary selection: elements of the beams
Secondary selection: inner facesheet
Magnitude type: Edge Contact
Conductance per Length: 2*523.8 W/(m·°C)
Coupling resolution: One-to-One
Only Connect Overlapping Elements check box is cleared

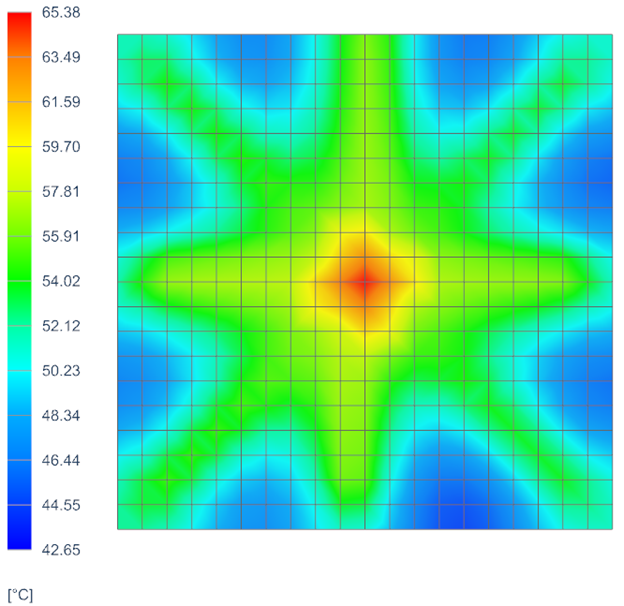
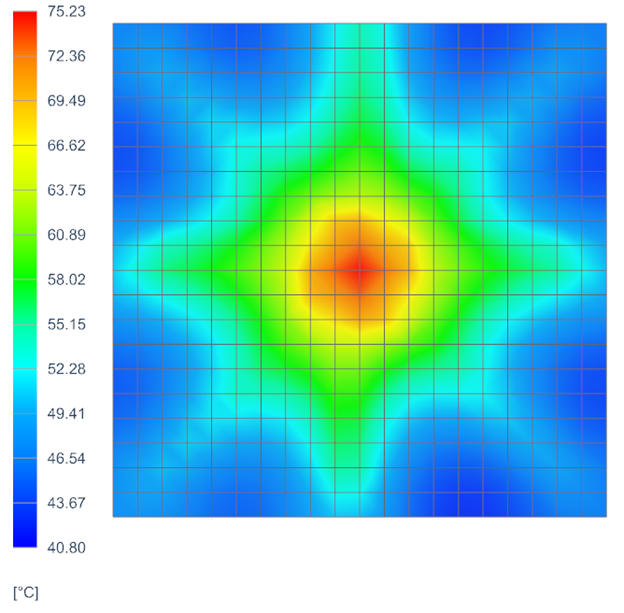
Temperature results

The maximum temperature is 65.38 ºC, which is much closer to the 53 ºC predicted when the load is distributed over the entire surface.

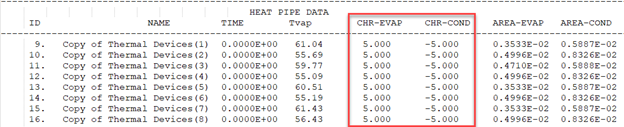
Include the PLOT BC SUMMARY Advanced Control simulation object to generate the <simulation name>-<solution name>data.html file to display the heat pipe fluid temperature, condenser and evaporator areas.

You can also include the Advanced Control simulation object with the DISPLAY BC SUMMARY TABLES advanced parameter to view which heat pipes are conducting more heat and if their placement is optimal.

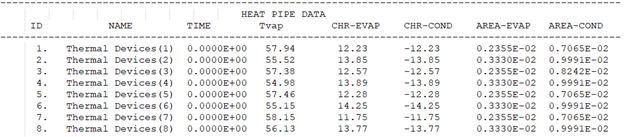
Understanding the heat pipe performance and effective length

From the evaporation and condenser areas, you can understand the performance of the heat pipe and determine its effective length. The following figure shows temperature profiles for two heat pipes: one attached to the panel along its full length and another attached only at each end.

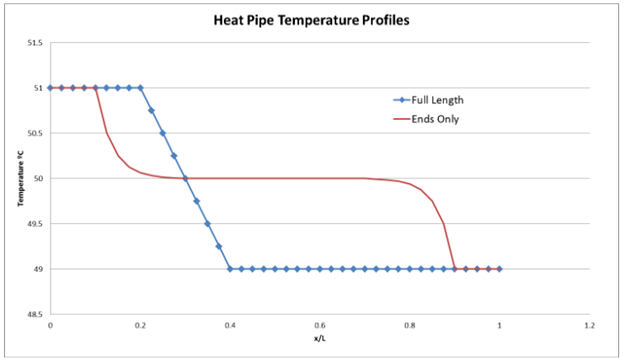
The fully attached pipe shows a region of linear temperature change between the hot and cold ends. This gradual change results from conduction along the pipe walls, blurring the delineation between the evaporator and condenser regions. Note that in practice, the transition will not be linear; it is shown this way to explain the concept. For the pipe with only the ends attached, there are similar transitions between each end and the adiabatic center section, which is at fluid temperature.

Fully attached heat pipe
Heat pipe attached at the ends

Notice the condenser area, AREA-COND, is much larger on the fully attached heat pipe, as observed in the preceding table, indicating better performance. It is also important to ensure that your design does not exceed the QL effective value specified by the heat pipe vendor. One way to do this is to use the Maximum Power Transport Limit optional setting. With this setting, the solver will cap the heat transferred in the heat pipe to the specified value. For example, if the heat pipe only has a 5 W*length, the results will be as follows:

Similarly, you should avoid boil-off or freezing limits. You can specify them using the Minimum Operating Temperature and Maximum Operating Temperature options. If the heat pipe fluid temperature reaches these temperatures, the solver stops transferring heat to the fluid node, and the heat pipe's solid structure is the only component conducting heat. For example, if you set the maximum temperature to 50 °C, you get the following temperature profile, which is the same temperature profile as when you don’t have the heat pipe simulation object but still have the 1D beams connected to the panel.