Card 9 - AXISYMM Axisymmetric Element Creation

KODE

KODE is the code AXISYMM (or 31)

N1

N1

• If N1 is a group name, all its elements are axisymmetric.
• If N1 = 0, the axisymmetry is global.

T1

T1 is the number of axisymmetric elements to be generated for radiation calculations for each axisymmetric element about the axis of revolution. T1 should be > 8 if radiation calculations are performed, default = 8. Axisymmetric elements may have 1 to 4 nodes.

T2

T2 is a code that defines the axis of revolution and plane in which the elements must lie. T2 is optional, if it is not present, the XZ option is used. The axis of revolution must be one of the global X, Y, or Z axes.

• T2 = XZ: the elements must be defined on the +X side of the XZ plane, and the rotation will be counterclockwise about the Z axis. This is the default.
• T2 = YZ: the elements must be defined on the +Y side of the YZ plane, and the rotation will be counterclockwise about the Z axis.
• T2 = XY: the elements must be defined on the +X side of the XY plane, and the rotation will be counterclockwise about the Y axis.
• T2 = ZY: the elements must be defined on the +Z side of the ZY plane, and the rotation will be counterclockwise about the Y axis.
• T2 = YX: the elements must be defined on the +Y side of the YX plane, and the rotation will be counterclockwise about the X axis.
• T2 = ZX: the elements must be defined on the +Z side of the ZX plane, and the rotation will be counterclockwise about the X axis.
• T2 = X: the elements and the X axis must lie on the same plane, and the rotation will be counterclockwise about the X axis.
• T2 = Y: the elements and the Y axis must lie on the same plane, and the rotation will be counterclockwise about the Y axis.
• T2 = Z: the elements and the Z axis must lie on the same plane, and the rotation will be counterclockwise about the Z axis.

Code example

 AXISYMM 0 8    
 $ THE THERMAL MODEL IS GLOBALLY AXISYMMETRIC WITH
 $ RESPECT TO THE GLOBAL Z AXIS.

Notes

1. Internal Element Generation for Radiation Calculations

For radiation calculations each 1- and 2-node axisymmetric element with an emissivity ≥ 0 generates T1 internal shell and beam elements in the counterclockwise direction about the axis of revolution. The first generated element is assigned the axisymmetric element number, the others are assigned to unused element numbers reported in the report log file. A 1-node axisymmetric element generates T1 beam elements, a 2-node axisymmetric element generates T1 shell elements. The generated elements are merged with the axisymmetric element once the radiation parameters have been calculated.

Hydraulic and 3 and 4-node elements are not expanded.

The Card 5d SPACE Card generates 3* T1 very large elements forming a closed cylinder about the origin for radiation calculations.

The radiative surface properties of the axisymmetric elements are passed to the generated elements.

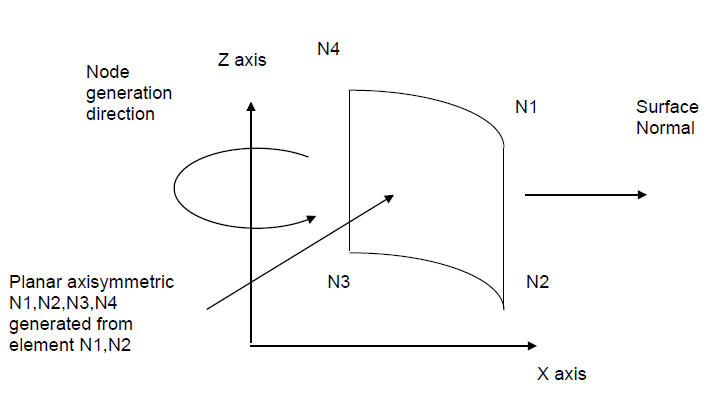
2. Surface Normals of Axisymmetric Elements

Care should be taken with radiation calculations that the surface normals point in the correct directions.

The direction of the surface normal of an expanded element is determined by the orientation of the nodes of its axisymmetric element with respect to the axis of revolution.

This is done by first identifying the direction vector of the axisymmetric element, which is from node 1 to node 2.

Next, the surface normal vector of the axisymmetric element is computed. This is the cross product (*) of the direction vector and the vector normal to the plane. For the default convention, the plane normal is the Y-axis, hence the element surface normal will be the direction vector*Y axis. The element surface normal lies in the XZ plane, and when it is revolved with the axisymmetric element it defines the orientations of the expanded element surface normals.

Another way of visualizing the surface normal direction of the axisymmetric element is that if the direction vector of the axisymmetric element points in the same direction as the axis vector (i.e. their dot products are positive), and the axisymmetric element lies in the +XZ plane, the surface normal points inwards towards the axis. If their dot products are negative (as in diagram), the surface normal points away from the axis. If their dot products are zero, then if the direction vector points in the +X direction, the surface normal points in the +Z direction, if the direction vector points in the –X direction, the surface normal points in the –Z direction.

If a 2-node axisymmetric shell elements lies on a solid, the surface normal of its front side will be automatically oriented so that it points out of the solid.

3. Physical Properties of Axisymmetric Elements

Special considerations apply to the PROP Cards:

For 1-node axisymmetric elements PROP BEAM should be specified.

For 2-node axisymmetric elements PROP SHELL should be specified.

For 3-4 node planar axisymmetric elements no PROP Card should be specified.

4. Additional Considerations

Axisymmetric elements are both geometrically and thermally axisymmetric with respect to the axis of revolution, i.e. there can be no tangential thermal gradients.

The model's symmetry is used to enhance the efficiency of the radiation calculations. Internally the Card 6 VFSALL/VFNALL Cards are replaced with equivalent VFS1ALL and VFN1ALL Cards. View factors are calculated only for the axisymmetric elements, the view factors for the expanded elements are generated from symmetry considerations. The view factors of the expanded elements are then merged.

If view factor calculations are requested with VFS1ALL or VFN1ALL Cards, the results may be erroneous, unless a VFSALL request is also present.

Circular elements may not be specified with XCIRC Cards for an axisymmetric model.

For conduction, capacitance, and Card 6e AREA Card calculations each axisymmetric element is assumed to have the fully revolved shape about the axis of revolution.

Elements may be specified to be non-axisymmetric with the Card 9 PARAM NOAXISYM Card.

If there is more than one AXISYMM card in the model, then the groups N1 must be exclusive.

If N1 = 0, then all elements that are not part of other AXISYMM cards will be expanded according to the global AXISYMM card.