Card 5b - Multiple Element Generation
This optional card generates the matrix of elements.
Parameters: KODE, NA, NB,
NDA, NDB, (NDVA(I), I = 1, MM),
(NDVB(I), I = 1, MM)
A Card 5b, following a Card 5a that creates a starting element, generates a matrix of NA*NB elements with the properties of the starting element.
KODE
KODE = GEN(or –5) generates elements on open surfaces and in open volumes (e.g., on flat or unclosed curved planes, rectangular volumes, and half cylinders).KODE = GENCL(or –6) generates elements on closed surfaces and in closed volumes (e.g. spheres, cylinders).
- The last (NAth) element's nodes in each row are joined to the nodes of the first element for each row to close the surface.
- Beam elements: the first node of the first element is joined to the second node of the NAth (last) element of each of the NB rows.
- Triangular elements: the first and third nodes of the first element are joined to the second and third nodes of the NAth element respectively. To approximate a circle with a series of triangular elements, the third node should fall on the center of the circle.
- Quad elements: the first and fourth nodes of the first element are joined to the second and third nodes of the NAth element respectively.
- Wedge elements: the first, third, fourth, and sixth nodes of the first element are joined to the second, third, fifth, and sixth nodes of the NA'th element respectively. If a solid cylinder is modeled with wedges, the third and sixth nodes of the wedges should fall on the axis of the cylinder.
- Hexahedra: the first, fourth, fifth, and eighth nodes of the first element are joined to the second, third, sixth, and seventh nodes of the NAth element respectively.
KODE = GENCLA(or –9) also generates elements on closed surfaces and volumes, but the nodes of the NAth element that are joined to the first element of each row differ from those of the GENCL option.
- Triangular elements: the second and third nodes of the first element are joined to the first and third nodes of the NAth element respectively. To approximate a circle with a series of triangular elements, the third node should fall on the center of the circle.
- Wedge elements: the first, second, and third nodes of the first element are joined to the fourth, fifth, and sixth nodes of the NAth element respectively.
- Hexahedra: the first, second, third, and fourth nodes of the first element are joined to the fifth, sixth, seventh and eighth nodes of the NAth element respectively.
NA
NA is the number of elements in the A direction (in a row).
NB
NB is the number of elements in the B direction (number of
rows).
NDA
NDA is the element number increment in the A direction.
NDB
NDB is the element number increment in the B direction.
NDVA(I)
NDVA(I) is the Ith node number increment in the A
direction.
NDVB(I)
NDVB(I) is the Ith node number increment in the B
direction.
MM
MM is the number of nodes of each element, which may be from 1 to 8,
and must equal the number of nodes of the starting element.
Code examples
Example 1: Quad elements in two rows of three are generated.
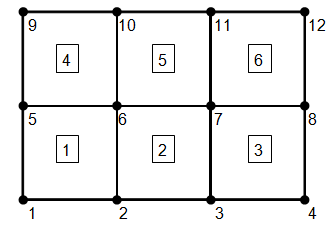
1 0 0 0 $ STARTING NODE
GEN 4 3 1 4 1 0 0 0 1 0 $ 4*3 NODES ARE GENERATED
–1
1 0 M1 0 P1 1 2 6 5 $ ELEMENT 1, STARTING CARD 5A ELEMENT
GEN 3 2 1 3 1 1 1 1 4 4 4 4
$ CARD 5B GENERATES 6 ELEMENTS IN 2 ROWS OF 3
Example 2: Six rectangular elements in two rows of three, defining a triangular cross-section tube.
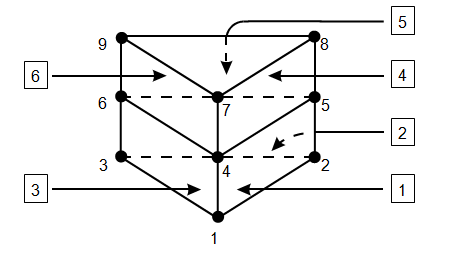
$ CYLINDRICAL COORDINATE SYSTEM DEFINED
SCYL
1 .577 0 0 $ STARTING NODE 1
$ 9 NODES GENERATED, 120 DEGREES APART, AT Z = 0, 1, AND 2.
GEN 3 3 1 3 0 120 0 0 0 1
–1
1 0 M1 0 P1 1 2 5 4 $ STARTING ELEMENT
GENCL 3 2 1 3 1 1 1 1 3 3 3 3 $ GENERATES 6 ELEMENTS IN 2 ROWS OF 3.
Example 3: Twelve rectangular elements in two rows of six, on the surface of a cylinder of radius 1 and height 2.
SCYL $ CYL. COORDINATE SYSTEM CARD 4C.
1 1 0 0 $ STARTING NODE 1
GEN 6 3 1 10 0 60 0 0 0 1
–1
1 0 M1 0 P1 1 2 12 11 $ STARTING ELEMENT 1
GENCL 6 2 1 10 1 1 1 1 10 10 10 10 $ CARD 4B GENERATES
$ $ 12 ELEMENTS, 1 THRU 6
$ $ AND 11 THRU 16.
