Card 6h - Symmetric Elements List

L

L is the code SYMNODES (or 16).

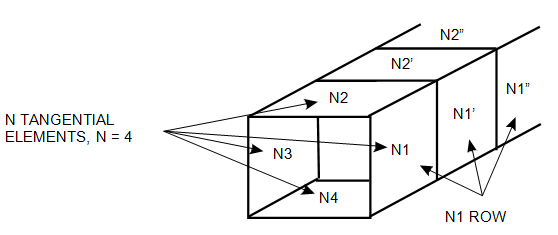
N1

N1 is the N1 row element.

N2, N3...NN

N2, N3...NN are the elements symmetrical with respect to the N1 row element. There is a maximum of 15 elements per Card, but Card 6o Continuation Cards may be used to extend this.

N1S, INC1, N1N, INC2, N2N

N1S, INC1, N1N, INC2, N2N

N1S is the Starting Element for Option 2. Option 2 creates N2N Cards 6h, each N1 row element incremented by INC2. Each Card 6h contains N1N elements, incremented by INC1. The generated cards have the format:

 SYMNODES, N1S, N1S+INC1, ....N1S+(N1N–1)*INC1
 SYMNODES, N1S+INC2, N1S+INC2+INC1,....N1S+INC2+(N1N–1)*INC1
 .
 .
 SYMNODES, N1S+(N2N–1)*INC2,.....N1S+(N2N–1)*INC2+(N1N–1)*INC1
            

Code example

 1 0 0 0                
 GEN 3 2 1 3 1 0 0 0 1 0
 GEN3RD 2 10 0 0 1
 $ CARD 4 NODES – THE CARTESIAN GLOBAL
 $ COORDINATE SYSTEM IS IN EFFECT
 –1
 1 0 M1 0 P1  1 11 12  2
 2 0 M1 0 P1 11 14 15 12
 3 0 M1 0 P1  4  5 15 14
 4 0 M1 0 P1  4  1  2  5
 11 0 M1 0 P1  2 12 13  3
 12 0 M1 0 P1 12 15 16 13
 13 0 M1 0 P1  5  6 16 15
 14 0 M1 0 P1  5  2  3  6
 $ CARD 5 ELEMENTS, 1,2,3,4 ARE SYMMETRIC,
 $ AND 11,12,13,14 ARE SYMMETRIC.
 –1
 SYMVREQ ARCOMB
 $ CARD 6G, THE ELEMENTS WILL BE MERGED,
 $ ONE CARD 6H PER STATION, ALL ELEMENTS ARE LISTED
 SYMNODES 1 2 3 4      $ ELEMENT 1 IS AN N1 ROW ELEMENT
 SYMNODES 11 12 13 14  $ ELEMENT 11 IS AN N1 ROW ELEMENT
 VFN1ALL 1             $ VIEW FACTORS FOR N1 ELEMENT 1
 VFN1ALL 11            $ VIEW FACTORS FOR N1 ELEMENT 11
 –1
 1 2 3 4               $ CARDS 7 MERGE ELEMENTS.
 11 12 13 14
 -1
 

Notes

For globally axisymmetric models see Card 9 - AXISYMM Axisymmetric Element Creation. Cards 6g and 6h need not be specified, they are automatically generated.

Cards 6g and 6h may be used for view factor calculations only, not for other types of radiation view factors.