Card 4b - Multiple Node Generation

KODE

KODE is the code GEN (or -5) generates a matrix of nodes.

NA, NB

NA is the number of nodes in the A direction.

NB is the number of nodes in the B direction.

NDA, NDB

NDA is the node number increment in the A direction, which must be ≥0.

NDB is the node number increment in the B direction, which must be ≥0.

DA1, DA2, DA3, DB1, DB2, DB3

DA1, DA2, DA3 are the (X, Y, Z) or (R, ϕ, Z) or (R, θ, ϕ) increments for the generated nodes in the A direction.

DB1, DB2, DB3 are the (X, Y, Z) or (R, ϕ, Z) or (R, θ, ϕ) increments for the generated nodes in the B direction

Code examples

Example 1 shows generation node from the starting point (1).

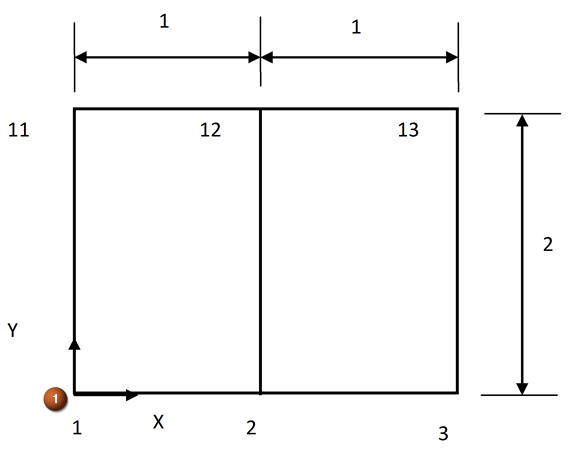
1 0 0 0
GEN 3 2 1 10 1 0 0 0 2 0
In a Cartesian coordinate system two cards Card 4a and Card 4b are equivalent to the following six Cards.
1 0 0 0
2 1 0 0
3 2 0 0
11 0 2 0
12 1 2 0
13 2 2 0

Example 2 shows two Cards Card 4a and Card 4b generate 6*3 nodes on the surface of a cylinder of unit radius at increments of PHI = 60 degrees and Z = 1 in a cylindrical coordinate system. Node numbers are incremented by 1 in the PHI direction and by 10 in the Z direction.

1 1 0 0
GEN 6 3 1 10 0 60 0 0 0 1

Example 3 shows two Cards Card 4a and Card 4b generate in a spherical coordinate system30 nodes on the surface of a sphere of unit radius at increments of ϕ=60 and θ=30. Node numbers are incremented by 1 in the ϕ direction and by 10 in θ direction.

1 1 30 0
GEN 6 5 1 10 0 0 60 0 30 0

Notes

A Card 4b following a Card 4a generates a matrix of NA*NB nodes. The nodes start with the coordinates and number of the Card 4a node. It is possible to generate nodes on a rectangular flat plane, a polar flat plane, a cylinder, a cone, a sphere, or other complex shapes.