VVT40 - Transient heat transfer in a model with a small Biot number
| Test case |
|---|
| SVTEST281 |
Description
This test validates the evolution of the surface temperature in a thin plate over time in the case of a small Biot number, where the internal temperature gradients are minimal due to dominant surface heat transfer.
Geometry
The model consists of a thin, squared 3D plate with dimensions of 100 by 100 mm and a thickness of 2 mm.
Simulation model
A 3D mesh is generated using linear hexahedron elements that are10 mm in size, arranged in two layers.

The meshed elements have the following material and physical properties:
- Shell material for the plate: Copper Alloy
- Mass density: ρ = 8000 kg/m3
- Specific heat at constant pressure: Cp = 385 J/kg·K
- Thermal conductivity: k = 0.3 W/m·°C
- Environmental fluid material: Air
- Mass density: ρ = 1.2041 kg/m3
- Specific heat at constant pressure: Cp = 1004.5 J/kg·K
The following boundary conditions are applied:
- Heat Flux type of Thermal Loads on the front surface of the plate with a heat flux of 100W/m2.
- Initial Temperature constraint on the whole plate of 20 °C.
- Thermal Convecting Zone on the back surface with the air temperature of 200 °C, the pressure of 0 Mpa, and a heat transfer coefficient of 2 W/(m2·°C).
This model uses the Simcenter 3D Multiphysics solver.
The following solver options are set:
- Solver = Simcenter 3D Multiphysics
The following solution options are set:
- Solution Control: Element Discretization is set to Finite Element Method in the Thermal Solution Parameters modeling object.
Theory
Since the Biot number is small, Bi < 0.1, it indicates that the internal thermal resistance within the solid is much lower than the thermal resistance at its surface. In this case, the temperature within the solid is assumed to be uniform at any given time during the heat transfer process. The lumped capacitance method can be used to find the temperature variation with time, based on the following assumptions:
- The temperature within the plate is spatially uniform meaning there are no temperature gradients inside the plate.
- The heat transfer is primarily governed by convection at the surface.
- The plate is small enough that internal conduction is much faster than heat loss to the surroundings.
The energy balance equation accounts for both external heating and convective cooling as follows:
Solving this differential equation yields the temperature evolution over time as follows:
where:
- a = q"A+hATf is the variable that combines effect of external heating and convective heat exchange with the fluid.
- q" is the flux applied to the surface of the plate.
- A is the surface area.
- Tf is the fluid ambient temperature.
- T0 is the initial temperature of the plate.
- h is the heat transfer coefficient.
- V is the volume of the plate.
- ρ is the density of the fluid.
- cp is the specific heat of the fluid.
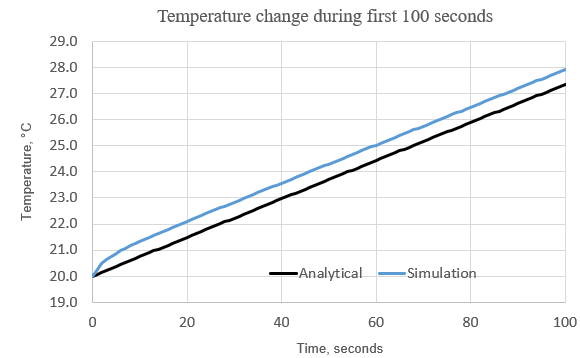
Results
The following graph compares the surface temperature for the first 100 seconds computed by the solver and the analytical solutions. The maximum temperature difference with the analytical solution is 0.6 °C.