VVT5 - Hollow sphere with convective boundary conditions
| Solution | Test case |
|---|---|
| Finite volume method | SVTEST6 |
| Finite element method | SVTEST232 |
Description
The purpose of this test case is to determine the inner and outer surface temperatures of a hollow sphere where both the inner and outer faces are subject to convective heat transfer.
Geometry
The solid geometry is created by revolving the sketch of half an annulus through an angle of 90 degrees. The inner radius of the annulus is ri = 300 mm, while the outer radius is ro = 392 mm. The result is a quarter hollow sphere. In addition, two datum planes are created by rotating copies of the XY plane ±2.5 degrees about the y-axis. The front face of the quarter sphere is subdivided using the referencing the revolved surface and the two datum planes. The following figure shows the model.
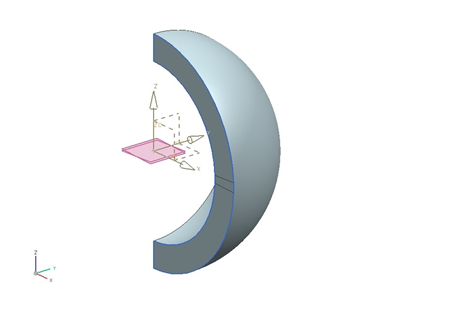
Simulation model
This model uses the Axisymmetric Thermal solution type.
The mesh is made of quadrilateral axisymmetric ZX shells using the mesh controls on the edges in order to generate five elements. The following figure shows that the elements are not the same size, but increase with radial distance.
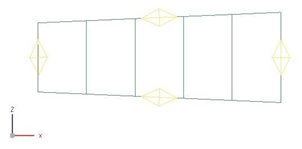
The meshed elements have the following material and physical properties:
- Thermal conductivity: k = 40.0 W/m·°C
- Mass density: arbitrary as this has no bearing on the analysis results
The following boundary conditions are applied:
- Convection to Environment constraint on the inner edge of the mesh with a heat transfer coefficient hi= 150 W/m2·°C and an ambient temperature T= 500 °C.
- Convection to Environment constraint on the outer edge of the mesh with a heat transfer coefficient h= 133.5 W/m2·°C and an ambient temperature T = 20 °C.
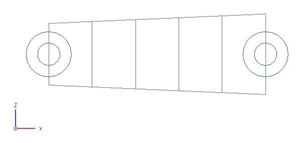
The following solution options are set:
- Solution Type = Steady State
- Results Options: Select the conductive heat fluxes at nodes and elements
The default solver parameters are selected.
Theory
Solving the heat equation expressed in spherical coordinates shows that the temperature within the solid material of the sphere is inversely proportionate to the radial location. The heat flow in the radial direction is constant. As such, this system can be viewed as a series network of thermal resistances between the ambient temperature within the hollow sphere and that outside the sphere. The thermal resistances due to convection within the sphere, due to conduction through the sphere, and due to convection outside the sphere are, respectively:
Then, the heat flow in the radial direction is given by:
The temperature at the inner and outer surfaces of the hollow sphere are computed as:
Results
The following table compares the nodal temperature results at the inner and outer surfaces, predicted by the thermal solver, with the calculated theoretical results. Simulation results are in agreement with theoretical values.
| Finite volume method | Finite element method | ||||
|---|---|---|---|---|---|
| Parameter | Ttheory (ºC) | Tsim (ºC) | Error (%) | Tsim (ºC) | Error (%) |
| T1 | 250.27 | 249.77 | 0.20 | 250.21 | 0.024 |
| T2 | 184.34 | 184.34 | 0.00 | 184.38 | 0.022 |
The table below shows the radial heat transfer rate, qr, obtained from the elemental heat fluxes. It is nearly constant, and comparable with the theoretical value.
| Finite volume method | Finite element method | |||||
|---|---|---|---|---|---|---|
| r (m) | qr",sim (W/m2) | qr,sim (W) | Error (%) | qr",sim (W/m2) | qr,sim (W) | Error (%) |
| 0.382 | 23003 | 42228 | 0.20 | 23008 | 42288 | 0.17 |
| 0.364 | 25389 | 42285 | 0.18 | 25390 | 42286 | 0.18 |
| 0.345 | 28167 | 42294 | 0.16 | 28162 | 42286 | 0.18 |
| 0.327 | 31428 | 42305 | 0.14 | 31413 | 42285 | 0.18 |
| 0.308 | 35290 | 42317 | 0.11 | 35262 | 42284 | 0.18 |
