VVT33 - Relative wall temperature on the edge of an axisymmetric plate
| Test case |
|---|
| SVTEST267 |
Description
The purpose of this validation test is to verify the total relative wall temperature of an axisymmetric plate using a fluid with temperature-dependent properties in a convection coupling boundary condition.
Geometry
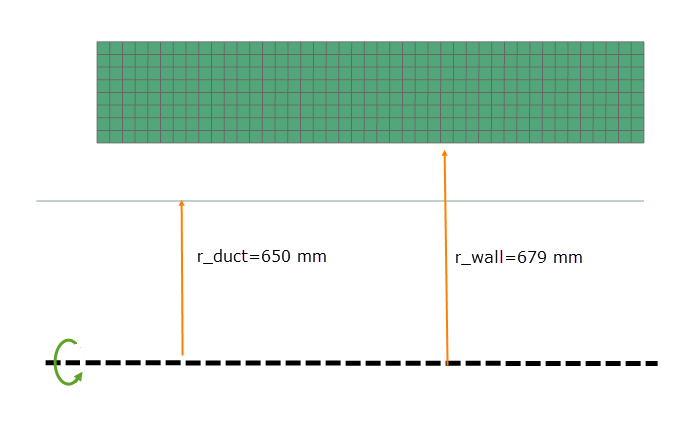
The axisymmetric modeling technique is used to model an axisymmetric plate with a length of 270 mm and a width of 50 mm. A green line between the axisymmetric plate and the axis of rotation is used to model a duct with a mass flow. The distances from the axis of rotation to the axisymmetric edge of the plate and the duct are 679 mm and 650 mm, respectively.
Simulation model
A 2D mesh is generated using axisymmetric linear quadrilateral elements each with a size of 6.25 mm. The axisymmetric duct is meshed using 1D elements.
The meshed elements have the following material and physical properties:
- Shell material for the plate: AISI_321
- Mass density: ρ = 7928 kg/m3
- Environmental fluid material: Air with temperature dependent properties
- Specific heat at constant pressure temperature dependent Cp(T). Linearisation of the specific heat gives the following linear dependence: Cp(T) = 0.1692 T + 946.31
The following boundary conditions are applied:
- Convection Coupling type of the Thermal
Coupling - Convection simulation object between the edge of the
plate and the duct with the heat transfer coefficient equal to 1e-6
tu/(hr·ft2·ºF)The rotational effects option is set to
Correct for Wall Rotation with the swirl ratio equal
to 0.1. The Adiabatic Wall Temperature for Heat Transfer
Calculations check box is selected.
Note that the fluid in the ducts is not heated by the solid body. This allows us to ignore additional heating and simplify the problem.
- Duct Fan/Pump type of Duct Flow Boundary Conditions applied to the duct with the mass flow of 1 lmb/s.
- Duct Total Pressure type of Duct Flow Boundary Conditions applied to the duct inlet with the total pressure of 384.53 psi.
- Duct Total Pressure type of Duct Flow Boundary Conditions applied to the duct exit with the total pressure of 384.53 psi.
- Temperature constraint applied to the inlet duct node with the temperature of 205 °F.
- Model Subset XY type of the Rotation load applied to the 2D plate with the angular velocity of 10000 rev/min.
- Thermal Convecting Zone load applied on the external edge of the 2D axisymmetric plate with the fluid temperature of 250 °F, pressure of 24 bars, the heat transfer coefficient of 0.01 Btu/(hr·ft2·ºF), and the swirl ratio equal to 0.5.
This model uses the Simcenter 3D Multiphysics solver.
The following solution parameters are set:
- Solution Control: Element Discretization is set to Finite Element Method in the Thermal Solution Parameters modeling object.
Theory
The total absolute and total relative temperatures are defined as follows when computing total temperature effects in heat transfer between the rotating fluid and the parts:
where:
- Tabs is the fluid total absolute temperature.
- Ts is the fluid static temperature.
- Trel is the fluid relative temperature.
- Vϕ=Xsωr is the absolute tangential velocity, where Χs is a swirl ratio, ω is a rotor speed, and r is an edge radius.
Thus, the following relationship between total absolute and relative temperatures is defined:
The specific heat is temperature-dependent, Cp=aT+b. Linearization between the total absolute and relative temperatures, is presented as follows.
In this problem, there is no additional heat input. Therefore, the total absolute temperature along the duct remains constant and is equal to the inlet fluid temperature. The only variable in the equation is the total relative temperature, which can be solved as a second-degree equation:
The total relative temperature can be resolved by using a2 = 0.1692 and b = 946.31 from specific heat relationship and Trel =559.29 ºF.
Results
The following table compares the axisymmetric plate's total relative wall temperature results predicted by the thermal solver with the calculated theoretical results. Simulation results are in agreement with theoretical values.
| Parameter | Theory | Simulation | Error (%) |
|---|---|---|---|
| Trel (℉) | 559.29 | 560.12 | 0.14 |
