Slip wall treatments for gases

For the flow regimes at low absolute pressure or in gas flows involving micro-channels, where the Knudsen number Kn is small, the no-slip boundary condition is no longer valid. The flow solver uses slip wall treatment for gas flows with Knudsen numbers ranging from 0.01 to 0.1:

where

L₀ is the characteristic length of the flow.
λ is the mean free path of the gas.

This regime is referred to as the slip regime, [43].

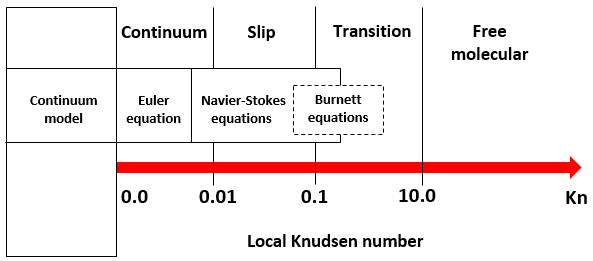
Schema of Continuum, Slip, Transition and Free Molecular flow regimes with a long horizontal arrow representing the Knudsen number labelled Kn displaying values 0.0, 0.01, 0.1, and 10. Two rectangles representing the Navier-Stokes equations and Burnett equations overlay the slip regime, located between 0.01 and 0.1.

Within this regime, the flow solver uses the standard momentum and energy equations to model the gas flow with the following modifications to the boundary treatments:

The velocity has a non-zero finite value, called slip velocity.
Thermal creep effects can be taken into account.
The gas temperature at the wall can be different from the wall temperature. There can be a temperature jump at the wall.

Slip velocity

The flow solver uses a second order extension of Maxwell’s model [44] to approximate the slip velocity. The traditional no-slip boundary condition is relaxed to allow the rarefied gas to slip at the wall by imposing a tangential component of the slip velocity at the solid boundary. The expression of the slip velocity is defined as:

where:

U_s is the slip velocity.
U_w is the wall velocity.
n is the local normal direction of the wall.
C₁ and C₂ represents respectively the first-order and second-order slip coefficients.

To impose the Maxwell model to all walls that have slip wall specified, use the USE LOW-PRESSURE MAXWELL SLIP WALL TREATMENT advanced parameter. This advanced parameter replaces the standard slip wall treatment by the Maxwell model.

By default, C₁ = 1 and C₂ = 0. You can specify them using the MAXWELL SLIP WALL C1 and MAXWELL SLIP WALL C2 advanced parameters.

You have to enable the Velocity Adjusted result set to view the results for the slip velocity. You can view the results in the slipValues.dat output file located in the run directory when you specify the OUTPUT LOW-PRESSURE MAXWELL SLIP WALL SUMMARY advanced parameter.

Thermal creep effect

The Maxwell's model with included thermal creep effect, induced in rarefied flow with large tangential wall temperature gradient is given by:

where

γ is the specific heat ratio defined as γ = c_p/c_v, where c_p is the specific heat at constant pressure and c_v is the specific heat at constant volume.
T is the absolute temperature of the gas.
s is the local tangential direction of the wall.
μ is the dynamic viscosity of the gas.
ρ is the density of the gas.

You can include the thermal creep effect only in the case of a non-isothermal fluid using the INCLUDE THERMAL CREEP TERM IN MAXWELL MODEL advanced parameter.

Temperature jump

The flow solver uses a temperature jump condition derived by von Smoluchowski [45] to account for the effect of gas temperature. The temperature jump expression is defined as:

where

T_s is the slip temperature of the gas.
T_w is the wall temperature.
σ_T is the thermal accommodation coefficient.
is the Prandtl number.
k is the thermal conductivity of the gas.

To impose the Maxwell low-pressure temperature jump model, use the USE LOW-PRESSURE MAXWELL TEMPERATURE JUMP TREATMENT advanced parameter. By default, the value for the thermal accommodation coefficient is 1. You can modify it using the MAXWELL SLIP WALL SIGMA T advanced parameter. Use the OUTPUT LOW-PRESSURE MAXWELL SLIP WALL SUMMARY advanced parameter to view the results in the slipValues.dat output file located in the run directory.

Mean free path of the gas

The mean free path of the gas is calculated locally at every wall-adjacent element by using the local gas density, pressure, and temperature.

where

T₀ is the specified reference temperature of the gas. You specify it using the REFERENCE TEMPERATURE FOR SLIP CORRECTION advanced parameter.
P₀ is the specified reference pressure of the gas. You specify it using the REFERENCE PRESSURE FOR SLIP CORRECTION advanced parameter.
S is the specified Sutherland constant for the viscosity of the gas. You specify it using the SUTHERLAND CONSTANT FOR SLIP CORRECTION advanced parameter.
λ₀ is the reference mean free path of the gas at temperature T₀ and pressure P₀, given by the following equation:

μ₀ is the reference viscosity of the ideal gas. You specify it using the REFERENCE VISCOSITY FOR SLIP CORRECTION advanced parameter.
ρ₀ is the reference density of the ideal gas, which is calculated using ideal gas law.
k_B is the Boltzmann constant.
η is the Avogadro's number.
R = 8.31434 (J/mol) is the universal gas constant.
R_g is the specific gas constant, which is obtained from the gas material properties.