Home
Flow Solver
Contains flow solver related guides, such as the reference and API guides.
Flow solver reference
Insert short description here
Modeling non-Newtonian fluid

Flow Solver
Contains flow solver related guides, such as the reference and API guides.
- Flow solver guides
  Maya HTT's flow solver is included and distributed with Simcenter 3D and Simcenter Femap. This page contains links to flow solver guides, which help you understand how the flow solver works.
- Flow solver reference
  Insert short description here
  - Introduction
    The flow solver computes a solution to the non-linear, partial differential equations for the conservation of mass, momentum, energy, and general scalars in general complex 3D geometries. It uses an element-based finite volume method and iterative Krylov methods to discretize and solve the governing equations.
  - Nomenclature
    The nomenclature table offers a description and sample units or constant values of the variables used in the Flow Solver Reference Manual.
  - Governing equations
    A model can be comprised of multiple flow enclosures. Each enclosure is a separate group of three-dimensional elements that form a separate fluid domain from the remaining geometry. The physical scales of each enclosure, such as the length scale, time scale, pressure, and temperature are independent of the other enclosures. The flow solver solves governing equations separately for each flow enclosure.
  - Source term
    The source term can represent body forces or flow resistance forces to model different physical phenomena.
  - Turbulence models
    In the flow solver, the flow field can be solved as laminar or as turbulent using governing equations.
  - Boundary conditions
    This section outlines different boundary conditions supported by the flow solver and the associated considerations.
  - Modeling a gas mixture
    The flow solver uses the scalar equation to model a gas mixed in any proportion with the main gas. The software supports up to five gases in the mixture. All gases are assumed to behave as ideal gases using the ideal gas law.
  - Modeling humidity
    The flow solver uses the gas mixture scalar equation to model humidity that is defined as a mixture of water vapor in air.
  - Modeling non-Newtonian fluid
  - Modeling particle tracking
    The following section describes the equations and forces that model particle trajectories, including treatment and effects of boundary conditions
  - Modeling fluid structure interaction
    Fluid structure interaction (FSI) computations account for motion or deformation of the solid structure boundaries that are interacting with the adjacent fluid flow. The flow solver handles both transient and static fluid structure interactions.
  - Discretization
    The following section describes the discretization methods used by the flow solver to discretize the governing equations.
  - Solver numerical methods
    The following section describes numerical methods used by the flow solver such as the linear equation solution, which acts as a preconditioning method to the basic iterative algorithm, and other solver methods, such as Krylov methods.
  - Flow solver files
    The following table describes the flow solver files, which are written in the run directory during the solving process.
  - Flow solver bibliography
    The following bibliography lists all sources used to explain how the flow solver works.
- Flow solver flowcharts
  This section consists of flowcharts that illustrate the methodology of the flow solver when you run a simple steady-state or transient simulation, and does not cover all features and situations. It also highlights how the flow solver is coupled to the thermal solver for a simple steady-state or transient coupled thermal-flow simulation.

Modeling non-Newtonian fluid

Non-Newtonian fluids

In non-Newtonian fluids, the shear stress of the fluid is not proportional to the rate of deformation. Therefore, the viscosity is no longer a constant and an additional model is required to model viscosity.

You can use one of the following models in accordance with fluid behavior:

Power-Law model for fluids with dilatant, pseudo-plastic, and similar behaviors.
Herschel-Bulkley modelfor fluids with Bingham plastic, viscoplastic, and similar behaviors.
Carreau model that is a generalized model that behaves as Newtonian at low shear rate and non-Newtonian for high shear rates.

Power-Law model

The fluid viscosity, μ, of a Power-Law fluid is defined in the flow solver using the following equation:

where:

K is the consistency index.
is the shear rate.
n is the power law index.
T₀ is the reference temperature.
T is the fluid temperature.
μ_min is the minimum viscosity limit.
μ_max is the maximum viscosity limit.

Herschel-Bulkley model

The fluid viscosity, μ, of a Herschel-Bulkley fluid is modelled in the flow solver using the following equation:

where:

K is the consistency index.
is the shear rate.
n is the power law index.
τ₀ is the yield stress.
τ_int is the stress value at the intersection point A shown in the following figure.
μ₀ is the yield viscosity or plastic viscosity.

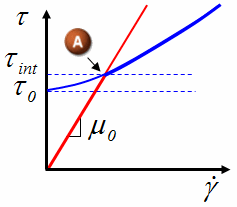
Line plot of the stress as a function of shear rate. A linear function with a positive slope, plotted in red, represents the yield viscosity. A convex curve, plotted in blue, has its intercept defined by the yield stress and intersects the red line.

To smooth convergence, a fluid defined with Herschel-Bulkley model, behaves like a Newtonian fluid until the local shear stress reaches intersect (A), shown as the red curve. The yield viscosity, μ₀, is a mathematical artefact introduced to improve convergence of the Herschel-Bulkley model when the stress is less than the yield stress. The blue curve shows the non-Newtonian Herschel-Bulkley behavior after intersect (A).

Carreau model

The fluid viscosity, μ, of a Carreau fluid is defined in the flow solver using the following equation:

where:

λ is the time constant.
is the shear rate.
n is the power law index.
T₀ is the reference temperature.
T is the fluid temperature.
μ_∞ is the infinite-shear viscosity.
μ₀ is the zero-shear viscosity.