Home
Flow Solver
Contains flow solver related guides, such as the reference and API guides.
Flow solver reference
Insert short description here
Boundary conditions
This section outlines different boundary conditions supported by the flow solver and the associated considerations.
Mixing plane
A mixing plane boundary condition interfaces two or more fluid volumes with different flow conditions.

Flow Solver
Contains flow solver related guides, such as the reference and API guides.
- Flow solver guides
  Maya HTT's flow solver is included and distributed with Simcenter 3D and Simcenter Femap. This page contains links to flow solver guides, which help you understand how the flow solver works.
- Flow solver reference
  Insert short description here
  - Introduction
    The flow solver computes a solution to the non-linear, partial differential equations for the conservation of mass, momentum, energy, and general scalars in general complex 3D geometries. It uses an element-based finite volume method and iterative Krylov methods to discretize and solve the governing equations.
  - Nomenclature
    The nomenclature table offers a description and sample units or constant values of the variables used in the Flow Solver Reference Manual.
  - Governing equations
    A model can be comprised of multiple flow enclosures. Each enclosure is a separate group of three-dimensional elements that form a separate fluid domain from the remaining geometry. The physical scales of each enclosure, such as the length scale, time scale, pressure, and temperature are independent of the other enclosures. The flow solver solves governing equations separately for each flow enclosure.
  - Source term
    The source term can represent body forces or flow resistance forces to model different physical phenomena.
  - Turbulence models
    In the flow solver, the flow field can be solved as laminar or as turbulent using governing equations.
  - Boundary conditions
    This section outlines different boundary conditions supported by the flow solver and the associated considerations.
    - Walls
      Understand the key equations used by the flow solver to treat different types of walls used as boundary conditions.
    - Fans
      In the flow solver, you can use Inlet Flow, Outlet Flow, Internal Fan, and Recirculation Loop fan types to model flow boundary conditions.
    - Openings
      Openings, also called vents, are pressure and temperature specified boundaries. The boundary condition imposed depends on the direction of the flow: inflow or an outflow. The direction of the flow at a vent can vary during the solve.
    - Convective outflow
      The convective outflow boundary condition models flow exiting the fluid domain without specifying the pressure. It lets the flow field exit and enter the flow domain on each element of the boundary as necessary conserving the mass.
    - Bursting membrane and flap
      The bursting membrane and flap boundary conditions model surfaces that open under specified pressure differences or time, allowing fluid flow.
    - High speed flow boundary condition
      You can use a high speed flow boundary condition for inlets or outlets, to specify the Mach number, pressure, and turbulence values at the domain boundary when the flow has velocities above Mach 0.3, which implies that the flow has density changes of more than 5% and is generally treated as compressible.
    - Screens
      The flow solver models planar resistances such as screens by calculating the pressure drop across them.
    - Symmetry boundaries
      A model is symmetric about a plane when the flow on one side of the plane is a mirror image of the flow on the opposite side of the plane. In such case, the use of a symmetry plane condition enables efficient use of computer resources by allowing the numerical solution to be obtained on a fraction of the original domain.
    - Periodic boundaries
      Periodic boundary conditions are used to simulate a flow leaving through a boundary A and entering through a boundary B under identical conditions (velocity, temperature, scalar values, etc).
    - Mixing plane
      A mixing plane boundary condition interfaces two or more fluid volumes with different flow conditions.
    - Rotating frames of reference
      The flow solver uses the frozen rotor method for rotating frames of reference (RFR). This method is useful for models where the flow distribution around the interface between the fixed and the rotating frames is non-uniform.
    - 1D network connected to 3D fluid region
      In a coupled thermal-flow analysis, you can couple a 3D fluid domain to a set of thermal streams and ducts with mass flow from a 1D fluid network that has the same fluid material. The flow solver solves the equations on the 3D fluid domain using the information from the 1D fluid network solved by the thermal solver.
  - Modeling a gas mixture
    The flow solver uses the scalar equation to model a gas mixed in any proportion with the main gas. The software supports up to five gases in the mixture. All gases are assumed to behave as ideal gases using the ideal gas law.
  - Modeling humidity
    The flow solver uses the gas mixture scalar equation to model humidity that is defined as a mixture of water vapor in air.
  - Modeling non-Newtonian fluid
  - Modeling particle tracking
    The following section describes the equations and forces that model particle trajectories, including treatment and effects of boundary conditions
  - Modeling fluid structure interaction
    Fluid structure interaction (FSI) computations account for motion or deformation of the solid structure boundaries that are interacting with the adjacent fluid flow. The flow solver handles both transient and static fluid structure interactions.
  - Discretization
    The following section describes the discretization methods used by the flow solver to discretize the governing equations.
  - Solver numerical methods
    The following section describes numerical methods used by the flow solver such as the linear equation solution, which acts as a preconditioning method to the basic iterative algorithm, and other solver methods, such as Krylov methods.
  - Flow solver files
    The following table describes the flow solver files, which are written in the run directory during the solving process.
  - Flow solver bibliography
    The following bibliography lists all sources used to explain how the flow solver works.
- Flow solver flowcharts
  This section consists of flowcharts that illustrate the methodology of the flow solver when you run a simple steady-state or transient simulation, and does not cover all features and situations. It also highlights how the flow solver is coupled to the thermal solver for a simple steady-state or transient coupled thermal-flow simulation.

Mixing plane

A mixing plane boundary condition interfaces two or more fluid volumes with different flow conditions.

The two interfacing faces:

Can have different geometries.
Can have a connected interface or be geometrically separated.
Do not need to be parallel.

The algorithm solves each fluid volume independently. It uses flow variable values from the adjacent fluid volume as boundary conditions.

You can use a mixing plane on two or more interfacing faces with different geometries. The interfacing faces are subdivided in a number of areas you specify. The areas are matched to its closest corresponding area according to their geometry and the averaging method you choose.


Averaging method examples
Along radius	Along vector
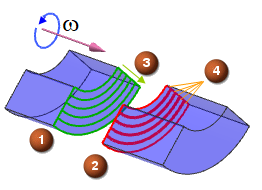
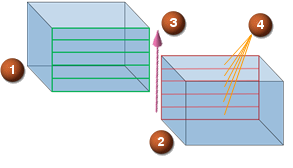
(1) Upstream (2) Downstream	(3) Averaging direction (4) Number of segments (for example: 5)

For each area, the averaged flow variables are transformed to a 1D field using an averaging technique and the information is applied to the other side as a boundary condition.

Depending on the flow direction, for the momentum equation along each area, the downstream static pressure is applied to the upstream side, whereas the total pressure of the upstream side is applied to the downstream side in an explicit order.

The values are mapped between areas to account for different geometry and mesh size at the interfaces.

You define either a radial or axial averaging method.

When the defined axis is perpendicular to the mixing plane, the flow variable values are averaged along radial arcs at the interfaces.
When the defined axis is parallel to the mixing plane, the flow variable values are averaged perpendicular to axial segments at the interfaces.