VVC2 - Condensation over a laminar flat plate
| Test case |
|---|
| SVTEST27 |
Description
This case examines the laminar flow of humid air that condensates over a flat plate. Water vapor cumulation is derived from the Chilton-Colburn [37] analogy that provides a relation between the heat transfer and the mass transfer over the plate. The Pohlhausen solution is used to compute the heat transfer over the flat plate. The computed results are compared with the solver solution.
The geometry is a rectangular prism, 25.4 mm in height, 10 mm in width and 304.8 mm in length.
Simulation model
The swept mesh is made of hexahedral elements. The following mesh controls are used:
- Height: 60 elements, 0.943 bias
- Width: 2 elements
- Length: 110 elements, 0.973 bias
The fluid is modeled using compressible air with the following properties:
- Mass density: ρ= 1.127 kg/m3
- Thermal conductivity: k= 0.027076 W/m·C
- Dynamic viscosity: µ = 1.9148e-005 Pa·s
- Specific heat at constant pressure: Cp= 1007.619585 J/kg·K
- Gas constant: R = 287 J/kg·K
The following boundary conditions are applied:
- Flow Boundary Condition: Inlet Flow on the front of the prism with a velocity of 5 m/s and ambient external conditions
- Flow Boundary Condition: Opening on the top and back of the prism
- Flow Surface: Boundary Flow Surface on the bottom surface using the No Slip Wall option with smooth wall friction and automatic convection properties
- Symmetry Plane on the right and left surfaces
- Temperature constraint on the bottom surface with a value of T = 0 °C
- Advanced Controls: Generic Entity with INPF Card type with the text input GPARAM 12 1526 0.5
This model uses the Advanced Thermal-Flow solution type with the following solution options:
- Turbulence Model: None (Laminar Flow)
- Solution Type: Transient
- Transient Setup: Start time = 0s, end time = 1 s, number of thermal time steps = 1000
- Ambient Conditions: Ambient fluid temperature = 40 °C, specific water vapor to dry air ratio = 0.02425
- Initial Conditions:
- 3D Flow group: X Velocity = 5 m/s
- 3D Flow group: Fluid Temperature = 40 °C
- 3D Flow group: Pressure = 0.101351 MPa
- Humidity, Tacer Fluids, and Mixtures group: Humidity = Specific
- Humidity, Tacer Fluids, and Mixtures group: Water Vapor to Dry Air Mass Ratio = 0.02425
The following solver parameters are selected:
- 3D Flow Solver: Maximum Residuals = 1e-6
- 3D Flow Solver: Global Heat Imbalance Fraction = 1e-6
- 3D Flow Solver: mass relaxation factor = 0.25
- 3D Flow Solver: global relaxation factor = 0.25
- Coupled Solver: Global Heat Imbalance Fraction = 1e-6
- Coupled Solver: Maximum temperature Change = 1e-5 Δ°C
Theory
The theory of Pohlhausen [38] and Chilton-Colburn [37] is used as a basis of comparison for the solver results. The Nusselt number and mass transfer coefficient are calculated using the following formulas:
where:
- Nux is the Nusselt number.
- hx is the heat transfer coefficient.
- x is the lengthwise position.
- k is the thermal conductivity of air.
- Pr is the Prandtl number of air.
- hmass is the mass transfer coefficient.
- ρ is the density of humid air.
- Cp is the specific heat of the humid air stream.
- DAB is the diffusion coefficient of water vapor in air.
- α is the thermal air diffusivity.
The rate of mass transfer of water vapor from air to the plate is given by:
where:
- ṁ is the rate of mass transfer.
- ρBsat is the saturation density of water in the air as a function of the temperature.
- Ts is the temperature of the condensate.
- ρBf is the water vapor density in the fluid element.
Therefore, the water accumulation on the plate can be computed as:
where:
- δ is the water cumulation.
- Δt is the total time.
Results
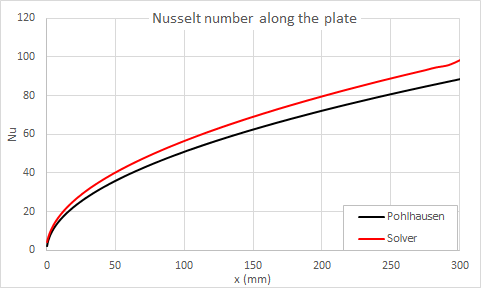
The following graph compares the Nusselt numbers predicted by the solver to the Pohlhausen theory.
The water cumulation at t = 1 s predicted by the solver is compared to the Chilton-Colburn theory.

