Home
Thermal Solver
Contains thermal solver related guides, such as the TMG reference manual, thermal API guide, and error message list.
Thermal solver theory
Describes the theory and methods of the thermal solver.
Radiation exchange methods
Thermal radiation is a heat transfer due to electromagnetic radiation emitted by the surface of bodies due to their temperature.
View factor calculation using ray-tracing
Angle dependent surface properties
This section explains how specular reflectivity or transmissivity is determined for elements based on the angle of incidence.

Thermal Solver
Contains thermal solver related guides, such as the TMG reference manual, thermal API guide, and error message list.
- Thermal solver guides
  Maya HTT's thermal solver is included in Simcenter 3D and in Simcenter Femap. This page contains links to thermal solver guides, which help you understand how the thermal solver works.
- Thermal solver theory
  Describes the theory and methods of the thermal solver.
  - Introduction
    This guide provides the theory and methods used by the thermal solver, including methods to calculate conduction, convection, and radiation, as well as modeling specific topics using the thermal solver.
  - Conduction methods
    To model heat conduction, the thermal solver can use two finite volume methods, center of element method or element's center of gravity method, or the finite element method.
  - Convective heat transfer methods
    The thermal solver computes convection conductances for various geometrical configurations using correlations that depend on specified characteristic lengths, convective surfaces, and type of convection.
  - Radiation exchange methods
    Thermal radiation is a heat transfer due to electromagnetic radiation emitted by the surface of bodies due to their temperature.
    - Basic view factor concepts
    - View factor calculation without ray-tracing
    - View factor calculation using ray-tracing
      - Ray-tracing methodology
        The following topic describes the thermal solver methodology for handling radiation in the presence of diffuse and transparent/specular surfaces using deterministic ray tracing method.
      - Ray-tracing with explicit planet modeling
      - Energy packet strength computation
        To compute the strength of the packets associated with the ray launched from DA_i, an incremental view factor DVF_ij between sub-elements DA_i and DA_j must be computed.
      - Accuracy consideration for ray-tracing
        Accuracy and performance of ray-tracing strongly depend on the elemental subdivision parameter, MESH.
      - Reflected/transmitted energy packet strengths computation
      - Angle dependent surface properties
        This section explains how specular reflectivity or transmissivity is determined for elements based on the angle of incidence.
      - Calculation of ray intercept and direction for curved elements
        This topic describes the procedure for calculating the local surface normal, the point of interception, and the new ray direction for curved elements.
      - Ray termination conditions
        This section outlines the circumstances under which ray termination occurs.
      - Summation of the energy packets to calculate the ray-traced view factors
        This section explains how energy packets are summed to calculate geometric view factors after ray-tracing calculations are completed.
      - Ray-tracing through solid elements
        This section describes the methodology for performing ray-tracing within solid elements when solar spectrum extinction or IR spectrum extinction coefficients are defined.
      - Reciprocity in ray-tracing
        This section explains how reciprocity is handled when calculating view factors with ray-tracing.
    - Plane stress view factor calculation when modeling with axisymetric or 3D elements
      This section explains how the thermal solver computes the view factor for axisymmetric or mixed 2D axi-3D models with plane stress elements for radiation requests.
  - Miscellaneous topics
  - References
- Thermal solver API guide
  Allows you to create or add functionality to enhance the thermal solver capabilities.

Angle dependent surface properties

This section explains how specular reflectivity or transmissivity is determined for elements based on the angle of incidence.

For some elements, specular reflectivity or transmissivity may be defined as a function of the angle of incidence. For these elements, the specular reflectivity or transmissivity is determined by linear interpolation of the data in the array referenced by the material property. If the incident angle falls outside the range defined in the array, the thermal solver uses the value at the nearest limit and does not extrapolate.

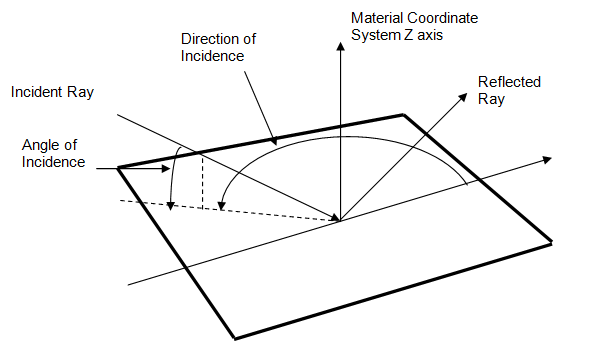
The direction of incidence is determined by projecting the ray onto the plane defined by the element surface normal and then determining the angle between this projection and the material orientation vector for the element. The angle of incidence is the angle between the incoming ray and the surface normal.

For specular elements j, the new direction is calculated by assuming the angle of incidence is equal to the angle of reflection with respect to the local surface normal.
For transparent elements j, if the indices of refraction on both sides of the element are not specified or are equal, the direction of the transmitted ray is the same as the incident ray. However, if the indices of refraction are specified and are different, then a new direction for the ray's travel is calculated using Snell's Law:

Where:

θ_inc is the angle the incident ray makes with the surface normal.
θ_trans is the angle the transmitted ray makes with the surface normal.
I_inc is the index of refraction on the incident side of the element.
I_trans is the index of refraction on the transmitted side of the element.

The index of refraction is assumed to be spectrum-independent, and the element j is assumed to have the same indices of refraction in both the IR and solar spectra.

If I_inc > I_trans (i.e., the ray goes from a dense to a less dense material), the computed sin(θ_trans) may be > 1. In this case, the material is assumed to reflect specularly, with the specular reflectivity equal to the transmissivity of the material.

If element j is planar, the local surface normal is the same as the surface normal of the element.