Creation of conductance matrix between boundary elements of a triangle

A conductance matrix is created between the boundary elements of the triangle, as shown in the example. The element geometry is on the left and the conductance matrix between boundary elements on the right.

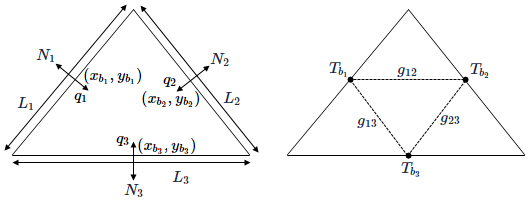
A linear internal temperature field, T(x,y), is defined within the triangle element as:

where a₁, a₂ and a₃ are coefficients.

The boundary element temperatures T_bj are defined at the midpoints of the edges as:

where j=1, 2, 3.

The weighting factors, e_ij, of the coefficients a₁, a₂ and a₃ are computed by substituting the boundary element temperatures into temperature field equation:

The unit normal vectors, N_i,on triangle edges, L_j, are defined based on the coordinates unit vectors i and j:

where b_j and c_j are coefficients of the edge unit normal vector.

The temperature gradient vector is constant over the triangle and is given as:

The heat flow, q_j, in each boundary element with the thickness of t, is defined using Fourier’s law:

Expanding and collecting terms from previous equations gives:

Using Kirchhoff's law, the heat flows between boundary elements, which are based on conductances, are given as:

where g_ij is the conductance between boundary elements i and j.

Conductances between boundary elements are given by equating the two previous equations: