Home
Thermal Solver
Contains thermal solver related guides, such as the TMG reference manual, thermal API guide, and error message list.
Thermal solver theory
Describes the theory and methods of the thermal solver.
Conduction methods
To model heat conduction, the thermal solver can use two finite volume methods, center of element method or element's center of gravity method, or the finite element method.
Finite volume methods
Element's center of gravity method
The element's center of gravity (CG) method creates conductances between the CG of the element and its boundary elements.
Conductance matrix for quadrilateral elements

Thermal Solver
Contains thermal solver related guides, such as the TMG reference manual, thermal API guide, and error message list.
- Thermal solver guides
  Maya HTT's thermal solver is included in Simcenter 3D and in Simcenter Femap. This page contains links to thermal solver guides, which help you understand how the thermal solver works.
- Thermal solver theory
  Describes the theory and methods of the thermal solver.
  - Introduction
    This guide provides the theory and methods used by the thermal solver, including methods to calculate conduction, convection, and radiation, as well as modeling specific topics using the thermal solver.
  - Conduction methods
    To model heat conduction, the thermal solver can use two finite volume methods, center of element method or element's center of gravity method, or the finite element method.
    - Finite volume methods
      - Comparison between finite volume methods
        The thermal solver supports two finite volume conduction methods—the center of element method and the element's center of gravity (CG) method—to create conductive conductances from geometry.
      - Element's center of gravity method
        The element's center of gravity (CG) method creates conductances between the CG of the element and its boundary elements.
        Conductance matrix for beams
        Conductance matrix for triangles
        Conductance matrix for tetrahedra
        Conductance matrix for quadrilateral elements
        Conductance matrix for wedge and hexahedron elements
        Conductance matrix for pyramid elements
        Interface conductances
      - Center of element method
        The following table lists element types supported by the center of element conduction method and how the thermal solver identifies their center of location and sub-elements to create conductances between elements.
      - Axisymmetric elements
        This topic describes how axisymmetric shell and solid elements are defined in thermal analysis.
      - Orthotropic materials
        This topic explains how orthotropic materials are handled in thermal analysis, detailing the process for stretching shell and solid elements based on their thermal conductivities in different material directions and the subsequent calculation of conductance.
    - Finite element method
      The finite element method computes the temperature values at discrete points, solid nodes, by solving the heat conduction equation.
  - Convective heat transfer methods
    The thermal solver computes convection conductances for various geometrical configurations using correlations that depend on specified characteristic lengths, convective surfaces, and type of convection.
  - Radiation exchange methods
    Thermal radiation is a heat transfer due to electromagnetic radiation emitted by the surface of bodies due to their temperature.
  - Miscellaneous topics
  - References
- Thermal solver API guide
  Allows you to create or add functionality to enhance the thermal solver capabilities.

Conductance matrix for quadrilateral elements

To calculate the conductance matrix, each quadrilateral element is divided into four triangle sub-elements, by connecting the corners to the CG of the quadrilateral element as shown in the example.

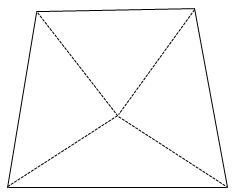
An additional four conductances, between the quadrilateral CG and boundary elements, are created by minimizing the root mean square value of the conductances between the boundary elements. Using the software default settings, conductance between the CG and boundary elements are balanced by:

where:

L_i is the length of the boundary element.
D_i is the distance between the element CG and the CG of the boundary element.
Θ_i is the angle between the line connecting the CG of the element to the boundary element and the surface normal of the boundary element.

The weighting factors for the conductances from the CG to the boundary elements are defined by assuming a parabolic temperature distribution within the element. The conductance matrix for quadrilateral elements has ten conductances.