Home
Flow Solver
Contains flow solver related guides, such as the reference and API guides.
Flow solver reference
Insert short description here
Boundary conditions
This section outlines different boundary conditions supported by the flow solver and the associated considerations.
Fans
In the flow solver, you can use Inlet Flow, Outlet Flow, Internal Fan, and Recirculation Loop fan types to model flow boundary conditions.
Fan boundary condition for energy equation
The flow solver allows you to specify different temperature boundary conditions depending on the type of fan used.

Flow Solver
Contains flow solver related guides, such as the reference and API guides.
- Flow solver guides
  Maya HTT's flow solver is included and distributed with Simcenter 3D and Simcenter Femap. This page contains links to flow solver guides, which help you understand how the flow solver works.
- Flow solver reference
  Insert short description here
  - Introduction
    The flow solver computes a solution to the non-linear, partial differential equations for the conservation of mass, momentum, energy, and general scalars in general complex 3D geometries. It uses an element-based finite volume method and iterative Krylov methods to discretize and solve the governing equations.
  - Nomenclature
    The nomenclature table offers a description and sample units or constant values of the variables used in the Flow Solver Reference Manual.
  - Governing equations
    A model can be comprised of multiple flow enclosures. Each enclosure is a separate group of three-dimensional elements that form a separate fluid domain from the remaining geometry. The physical scales of each enclosure, such as the length scale, time scale, pressure, and temperature are independent of the other enclosures. The flow solver solves governing equations separately for each flow enclosure.
  - Source term
    The source term can represent body forces or flow resistance forces to model different physical phenomena.
  - Turbulence models
    In the flow solver, the flow field can be solved as laminar or as turbulent using governing equations.
  - Boundary conditions
    This section outlines different boundary conditions supported by the flow solver and the associated considerations.
    - Walls
      Understand the key equations used by the flow solver to treat different types of walls used as boundary conditions.
    - Fans
      In the flow solver, you can use Inlet Flow, Outlet Flow, Internal Fan, and Recirculation Loop fan types to model flow boundary conditions.
      - Fan boundary condition for energy equation
        The flow solver allows you to specify different temperature boundary conditions depending on the type of fan used.
      - Fan boundary condition for scalar equation
        The flow solver allows you to specify values of mass ratio, as well as relative or specific humidity at inlet flows.
      - Pressure rise
        In the context of a fan curve the term pressure rise, often referred to as delta pressure, is a fundamental parameter that plays a pivotal role in understanding the performance characteristics of a fan system. Learn how the flow solver models pressure rise for inlet, outlet, internal, and recirculation fans.
      - Fan Curve
        The flow solver defines the fan volume flow rate for all types of fan curves using either or both implicit and explicit approaches.
      - Flow direction
        The flow imposed on inlet or internal fans can be specified to be at an angle from the fan normal or as a swirl with a defined axis of rotation and at a certain angle from the fan normal.
    - Openings
      Openings, also called vents, are pressure and temperature specified boundaries. The boundary condition imposed depends on the direction of the flow: inflow or an outflow. The direction of the flow at a vent can vary during the solve.
    - Convective outflow
      The convective outflow boundary condition models flow exiting the fluid domain without specifying the pressure. It lets the flow field exit and enter the flow domain on each element of the boundary as necessary conserving the mass.
    - Bursting membrane and flap
      The bursting membrane and flap boundary conditions model surfaces that open under specified pressure differences or time, allowing fluid flow.
    - High speed flow boundary condition
      You can use a high speed flow boundary condition for inlets or outlets, to specify the Mach number, pressure, and turbulence values at the domain boundary when the flow has velocities above Mach 0.3, which implies that the flow has density changes of more than 5% and is generally treated as compressible.
    - Screens
      The flow solver models planar resistances such as screens by calculating the pressure drop across them.
    - Symmetry boundaries
      A model is symmetric about a plane when the flow on one side of the plane is a mirror image of the flow on the opposite side of the plane. In such case, the use of a symmetry plane condition enables efficient use of computer resources by allowing the numerical solution to be obtained on a fraction of the original domain.
    - Periodic boundaries
      Periodic boundary conditions are used to simulate a flow leaving through a boundary A and entering through a boundary B under identical conditions (velocity, temperature, scalar values, etc).
    - Mixing plane
      A mixing plane boundary condition interfaces two or more fluid volumes with different flow conditions.
    - Rotating frames of reference
      The flow solver uses the frozen rotor method for rotating frames of reference (RFR). This method is useful for models where the flow distribution around the interface between the fixed and the rotating frames is non-uniform.
    - 1D network connected to 3D fluid region
      In a coupled thermal-flow analysis, you can couple a 3D fluid domain to a set of thermal streams and ducts with mass flow from a 1D fluid network that has the same fluid material. The flow solver solves the equations on the 3D fluid domain using the information from the 1D fluid network solved by the thermal solver.
  - Modeling a gas mixture
    The flow solver uses the scalar equation to model a gas mixed in any proportion with the main gas. The software supports up to five gases in the mixture. All gases are assumed to behave as ideal gases using the ideal gas law.
  - Modeling humidity
    The flow solver uses the gas mixture scalar equation to model humidity that is defined as a mixture of water vapor in air.
  - Modeling non-Newtonian fluid
  - Modeling particle tracking
    The following section describes the equations and forces that model particle trajectories, including treatment and effects of boundary conditions
  - Modeling fluid structure interaction
    Fluid structure interaction (FSI) computations account for motion or deformation of the solid structure boundaries that are interacting with the adjacent fluid flow. The flow solver handles both transient and static fluid structure interactions.
  - Discretization
    The following section describes the discretization methods used by the flow solver to discretize the governing equations.
  - Solver numerical methods
    The following section describes numerical methods used by the flow solver such as the linear equation solution, which acts as a preconditioning method to the basic iterative algorithm, and other solver methods, such as Krylov methods.
  - Flow solver files
    The following table describes the flow solver files, which are written in the run directory during the solving process.
  - Flow solver bibliography
    The following bibliography lists all sources used to explain how the flow solver works.
- Flow solver flowcharts
  This section consists of flowcharts that illustrate the methodology of the flow solver when you run a simple steady-state or transient simulation, and does not cover all features and situations. It also highlights how the flow solver is coupled to the thermal solver for a simple steady-state or transient coupled thermal-flow simulation.

Fan boundary condition for energy equation

The flow solver allows you to specify different temperature boundary conditions depending on the type of fan used.

Specified temperature

The fluid temperature can be specified as a boundary value on inlet flow only. The temperature imposed can either be the ambient temperature or specified temperature.

Temperature change from extract to return

For recirculation loop, you can specify a temperature change, ΔT, from the extract side of the fan to the return side of the fan as:

This is equivalent to specifying the value of the return temperature, T_return:

Heat generation

The heat generation condition is in fact applied as a temperature specification at the exhaust side, T_extract, or return side, T_return, of the fan.

Heat generation can be specified on internal fans as well as on recirculation loops. The amount of heat generated by the fan can be expressed as:

ṁ is the mass flow rate through the fan.
C_p is the specific heat at constant pressure of the fluid.
ΔT = T_exhaust - T_intake for internal fans.
ΔT = T_return - T_extract for recirculation loops.

Convective heat exchange

When calculating a temperature change due to a convective heat exchange, the flow solver makes the following assumptions:

A virtual duct connects the extract side to the return side.
The duct walls are in perfect contact with the environment maintained at a specified temperature T_w.
There is a fully developed laminar flow in the duct.

The flow solver models a device or system that extracts fluid from the 3D flow domain and injects the same fluid back into the domain. On the following figure, the virtual duct is between the model's 3D flow domains delimited by dashed planes.

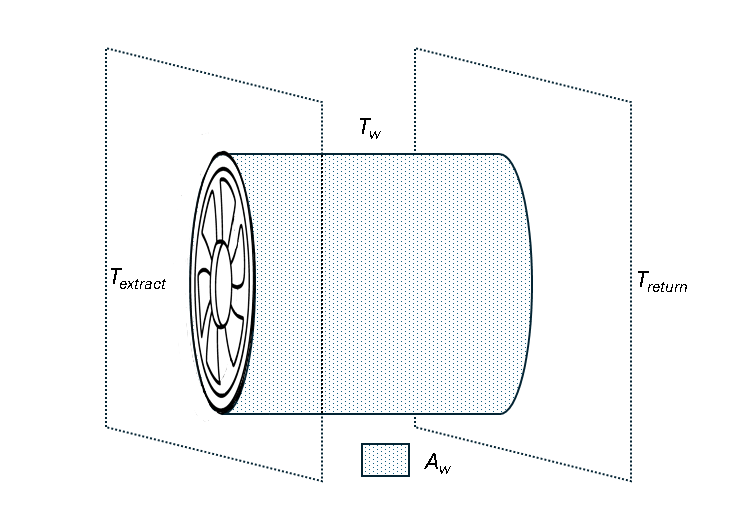
Diagram of a fan moving fluid through a duct. The fluid starts at extract temperature and ends at the return temperature.

Under these assumptions, the heat transfer is governed by the log-mean temperature difference equation:

where:

A_w is the duct wall surface area.
h is the convective heat transfer coefficient.

The following diagram shows how the fluid return temperature changes along the length of the duct as it flows through the duct, gradually approaching the wall temperature due to convective heat exchange. In this example, T_extract < T_return, though the opposite case is also possible.