Home
Flow Solver
Contains flow solver related guides, such as the reference and API guides.
Flow solver reference
Insert short description here
Discretization
The following section describes the discretization methods used by the flow solver to discretize the governing equations.
Spatial discretization
This section describes the spatial discretization of the governing equations and the terms that compose them.
Shape function
The flow solver computes solution variables, such as velocity components, pressure, and temperature at the mesh nodes. It then approximates the solution variables at arbitrary points in the computational domain with shape functions. The shape functions interpolate solution variables from mesh nodes to the arbitrary point with given nodal solution variables, and the coordinates of an arbitrary point in the computational domain.

Flow Solver
Contains flow solver related guides, such as the reference and API guides.
- Flow solver guides
  Maya HTT's flow solver is included and distributed with Simcenter 3D and Simcenter Femap. This page contains links to flow solver guides, which help you understand how the flow solver works.
- Flow solver reference
  Insert short description here
  - Introduction
    The flow solver computes a solution to the non-linear, partial differential equations for the conservation of mass, momentum, energy, and general scalars in general complex 3D geometries. It uses an element-based finite volume method and iterative Krylov methods to discretize and solve the governing equations.
  - Nomenclature
    The nomenclature table offers a description and sample units or constant values of the variables used in the Flow Solver Reference Manual.
  - Governing equations
    A model can be comprised of multiple flow enclosures. Each enclosure is a separate group of three-dimensional elements that form a separate fluid domain from the remaining geometry. The physical scales of each enclosure, such as the length scale, time scale, pressure, and temperature are independent of the other enclosures. The flow solver solves governing equations separately for each flow enclosure.
  - Source term
    The source term can represent body forces or flow resistance forces to model different physical phenomena.
  - Turbulence models
    In the flow solver, the flow field can be solved as laminar or as turbulent using governing equations.
  - Boundary conditions
    This section outlines different boundary conditions supported by the flow solver and the associated considerations.
  - Modeling a gas mixture
    The flow solver uses the scalar equation to model a gas mixed in any proportion with the main gas. The software supports up to five gases in the mixture. All gases are assumed to behave as ideal gases using the ideal gas law.
  - Modeling humidity
    The flow solver uses the gas mixture scalar equation to model humidity that is defined as a mixture of water vapor in air.
  - Modeling non-Newtonian fluid
  - Modeling particle tracking
    The following section describes the equations and forces that model particle trajectories, including treatment and effects of boundary conditions
  - Modeling fluid structure interaction
    Fluid structure interaction (FSI) computations account for motion or deformation of the solid structure boundaries that are interacting with the adjacent fluid flow. The flow solver handles both transient and static fluid structure interactions.
  - Discretization
    The following section describes the discretization methods used by the flow solver to discretize the governing equations.
    - Control-volume method
      The flow solver uses a finite-element based control-volume method for discretization of the governing equations. With this method, the governing equations are integrated over a control volume and over a time step.
    - Spatial discretization
      This section describes the spatial discretization of the governing equations and the terms that compose them.
      - Governing equations discretization
        Understand how the mass, momentum, and energy equations are discretized and used by the flow solver.
      - Diffusion terms
        The general form of the diffusion term involves evaluating the derivative of a field variable at an integration point using shape functions. For a given node, the flow solver calculates the field variable using shape functions, which are polynomials determined by the flow solver.
      - Pressure term
        Understand how the flow solver computes the pressure term.
      - Convective terms
        The discretized convective terms are evaluated using nodal values with first or higher-order schemes. Higher order schemes offer more precision but are less stable.
      - Shape function
        The flow solver computes solution variables, such as velocity components, pressure, and temperature at the mesh nodes. It then approximates the solution variables at arbitrary points in the computational domain with shape functions. The shape functions interpolate solution variables from mesh nodes to the arbitrary point with given nodal solution variables, and the coordinates of an arbitrary point in the computational domain.
        Skewed element treatment
        The flow solver uses the finite element method to compute the gradient of the solution field for mesh elements. To improve the solution quality for skewed elements, it uses the finite difference method.
    - Temporal discretization
      The flow solver uses the Backward Euler and Crank-Nicolson schemes, and the local time step method as time discretization methods.
    - Other discretization methods
      The following section describes discretization methods such as the disjoint mesh pairing method, the immersed boundary, or various mesh moving methods.
  - Solver numerical methods
    The following section describes numerical methods used by the flow solver such as the linear equation solution, which acts as a preconditioning method to the basic iterative algorithm, and other solver methods, such as Krylov methods.
  - Flow solver files
    The following table describes the flow solver files, which are written in the run directory during the solving process.
  - Flow solver bibliography
    The following bibliography lists all sources used to explain how the flow solver works.
- Flow solver flowcharts
  This section consists of flowcharts that illustrate the methodology of the flow solver when you run a simple steady-state or transient simulation, and does not cover all features and situations. It also highlights how the flow solver is coupled to the thermal solver for a simple steady-state or transient coupled thermal-flow simulation.

Shape function

The flow solver computes solution variables, such as velocity components, pressure, and temperature at the mesh nodes. It then approximates the solution variables at arbitrary points in the computational domain with shape functions. The shape functions interpolate solution variables from mesh nodes to the arbitrary point with given nodal solution variables, and the coordinates of an arbitrary point in the computational domain.

The shape function representation is:

where:

ϕ_i is the solution value at node N^e_i.
B_i is the finite element shape function associated with the same node.

The flow solver uses two types linear-linear and tri-linear shape functions for its interpolation approximations. The following figure depicts the locations of the x_ip employed in conjunction with the expansion of the shape function for the quadrature of integration surface A_ip.

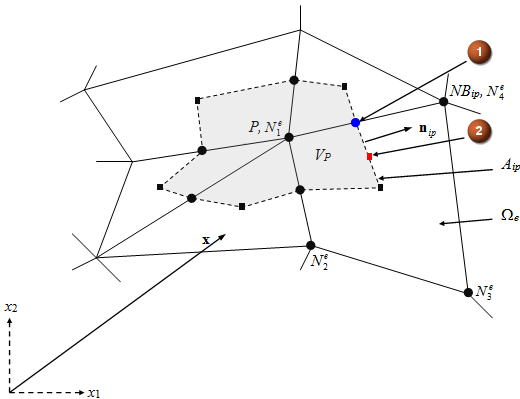
Diagram of control volume finite element discretization depicting triangular and quadrilateral elements. The integration surface is shaded in light grey.

(1) Location x_ip for linear-linear interpolation

(2) Location x_ip for tri-linear interpolation

The shape functions always represent a tri-linear interpolation over element to the arbitrary point .

The linear-linear shape function imposes a selection for lying at the midpoint of the vector, which joins node with its neighbor across A_ip. The values of ϕ(x_ip) and the directional derivative along the vector , are reduced to the following approximations:

By default, the flow solver is set to low resolution mode and uses linear-linear shape functions. When you choose high resolution mode, the flow solver uses tri-linear functions.