Home
Thermal Solver
Contains thermal solver related guides, such as the TMG reference manual, thermal API guide, and error message list.
Thermal solver theory
Describes the theory and methods of the thermal solver.
Radiation exchange methods
Thermal radiation is a heat transfer due to electromagnetic radiation emitted by the surface of bodies due to their temperature.
View factor calculation without ray-tracing
View factor accuracy considerations
The accuracy of the Nusselt sphere technique is compared with the contour integral technique and the double summation technique.

Thermal Solver
Contains thermal solver related guides, such as the TMG reference manual, thermal API guide, and error message list.
- Thermal solver guides
  Maya HTT's thermal solver is included in Simcenter 3D and in Simcenter Femap. This page contains links to thermal solver guides, which help you understand how the thermal solver works.
- Thermal solver theory
  Describes the theory and methods of the thermal solver.
  - Introduction
    This guide provides the theory and methods used by the thermal solver, including methods to calculate conduction, convection, and radiation, as well as modeling specific topics using the thermal solver.
  - Conduction methods
    To model heat conduction, the thermal solver can use two finite volume methods, center of element method or element's center of gravity method, or the finite element method.
  - Convective heat transfer methods
    The thermal solver computes convection conductances for various geometrical configurations using correlations that depend on specified characteristic lengths, convective surfaces, and type of convection.
  - Radiation exchange methods
    Thermal radiation is a heat transfer due to electromagnetic radiation emitted by the surface of bodies due to their temperature.
    - Basic view factor concepts
    - View factor calculation without ray-tracing
      - View factor calculation algorithm
        The following outlines the steps by which view factors are calculated without ray-tracing using deterministic method without explicit sky modeling.
      - View factor accuracy considerations
        The accuracy of the Nusselt sphere technique is compared with the contour integral technique and the double summation technique.
      - Inaccuracies due to non-uniform illumination
        Radiation calculations with view factors assume uniform illumination over an element, and potentially significant errors may be introduced when this assumption is not fulfilled.
      - Planet view factor calculation without ray-tracing
        The planet view factor is the element's view factor to the planet.
      - Albedo factors calculation without ray-tracing
    - View factor calculation using ray-tracing
    - Plane stress view factor calculation when modeling with axisymetric or 3D elements
      This section explains how the thermal solver computes the view factor for axisymmetric or mixed 2D axi-3D models with plane stress elements for radiation requests.
  - Miscellaneous topics
  - References
- Thermal solver API guide
  Allows you to create or add functionality to enhance the thermal solver capabilities.

View factor accuracy considerations

The accuracy of the Nusselt sphere technique is compared with the contour integral technique and the double summation technique.

The following table compares the percentage error when calculating view factor of two parallel unit squares separated by a distance D for the contour integral technique, the Nusselt sphere technique with the subdivision parameters MESH = 1 and MESH = 2, and another popular technique called the double summation technique, which is not used in the thermal solver.


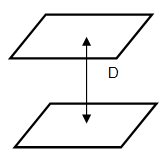
Technique	Contour integral	Nusselt sphere		Double summation
D		MESH = 1	MESH = 2	MESH = 1	MESH = 2
0.01	0.001	1.9	0.001	80000.	20000.
0.1	0.0002	10.6	4.7	865.	158.
1.	0.000005	5.6	1.3	8.5	1.94
10.	0	0.1	0.02	0.165	0.04

As the table shows, the accuracy of the contour integral technique is almost totally independent of geometry. The Nusselt sphere technique has an error upper bound around 11% for MESH = 1, and 5% for MESH = 2, occurring when the elements are very close together. The double summation technique breaks down when the elements are very close together, unless they are divided into much smaller sub-elements.