Temperature error estimates
Temperature error estimates are used for adaptive meshing to determine areas where mesh refinement is needed to ensure solution accuracy. The mesh is refined in regions where the temperature error estimate exceeds a predefined tolerance, improving the solution.
Using finite element method
When the model uses the finite element method, the thermal solver uses a posteriori error estimation technique that evaluates the error based on the computed temperatures at nodes after the solve. Then, based on the nodal error estimates, the solver computes elemental temperature error estimates.
The thermal solver applies the following algorithm to compute temperature error estimates.
The thermal solver computes the integration point temperature gradient for each integration point IP of each element E by interpolating the nodal temperatures using shape function gradients as:
where T1, T2, T3, ... are the temperature at nodes 1,2,3, ..., and ξ1, ξ2, ξ3, ... are the nodal shape functions computed at the integration point IP. For more information, see Finite element integration points and shape functions.
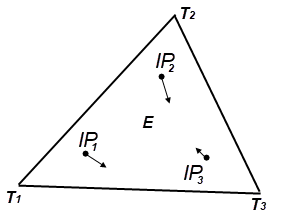
The solver extrapolates the integration point temperature gradients of element E to all nodes N belonging to E, obtaining ∇T(N,E), by using the singular value decomposition (SVD) method. This is done for every element in the model. Temperature gradients at nodes indicate the direction and steepness of the highest temperature increase occurring at the node's location. As a result, for each node that is shared with multiple elements, there is as many temperature gradients as elements sharing the node.
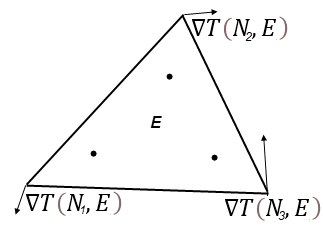
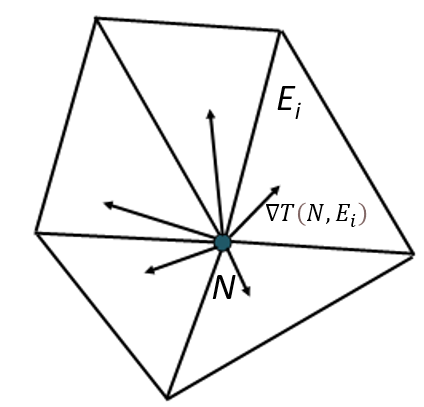
For each node N, the solver computes the L2 norm for all pairs of temperature gradients to measure the length of the difference between the gradients in the pair.
-
It finds the maximum temperature gradient difference between all pairs of temperature gradients, as it indicates the largest gradient variation at node N.
- The solver estimates the temperature error based on the identified maximum temperature gradient difference for the node N as:
where:
- <L> is the mean length of all element edges adjacent to the node N.
- is the correction factor obtained by comparing temperature results of the simulation with the analytical solution.
Using finite volume method
When the model uses the finite volume method, the error estimation algorithm is based on improved solution heuristic [6]. The estimates defined for the algorithm are the differences between the computed and the improved solution. To obtain an improved solution that is continuous in the whole model, the nodal temperatures obtained by the solver are used. The nodal temperatures include pertinent information about the surrounding computed temperatures and heat fluxes.
The error estimate is calculated as follows:
For each element E, the software defines the error estimate Est(BE) as the maximum over all boundary elements BE of E.
Where Est(BE)=absolute difference between:
- The improved solution value at BE, which is obtained by linearly interpolating the nodal values of all the nodes of BE.
- The computed solution temperature at BE.
For each elemental error estimation, only data local to the element are used.
