Home
Thermal Solver
Contains thermal solver related guides, such as the TMG reference manual, thermal API guide, and error message list.
Thermal solver theory
Describes the theory and methods of the thermal solver.
Conduction methods
To model heat conduction, the thermal solver can use two finite volume methods, center of element method or element's center of gravity method, or the finite element method.
Finite element method
The finite element method computes the temperature values at discrete points, solid nodes, by solving the heat conduction equation.
Finite element integration points and shape functions
Integration points and shape functions for different type of elements are predefined in the thermal solver and allow the discretization of a continuous domain and the approximation of its behavior using finite elements.

Thermal Solver
Contains thermal solver related guides, such as the TMG reference manual, thermal API guide, and error message list.
- Thermal solver guides
  Maya HTT's thermal solver is included in Simcenter 3D and in Simcenter Femap. This page contains links to thermal solver guides, which help you understand how the thermal solver works.
- Thermal solver theory
  Describes the theory and methods of the thermal solver.
  - Introduction
    This guide provides the theory and methods used by the thermal solver, including methods to calculate conduction, convection, and radiation, as well as modeling specific topics using the thermal solver.
  - Conduction methods
    To model heat conduction, the thermal solver can use two finite volume methods, center of element method or element's center of gravity method, or the finite element method.
    - Finite volume methods
    - Finite element method
      The finite element method computes the temperature values at discrete points, solid nodes, by solving the heat conduction equation.
      - Finite element space discretization
      - Finite element time discretization
      - Finite element mesh
        To solve conduction heat transfer in a solid domain, a mesh is essential when using the finite element method.
      - Finite element integration points and shape functions
        Integration points and shape functions for different type of elements are predefined in the thermal solver and allow the discretization of a continuous domain and the approximation of its behavior using finite elements.
      - Axisymmetric finite element formulation
      - Modeling immersed ducts with the finite element method
        When a model with immersed ducts is solved using the finite element method, the thermal solver uses the algorithm described in the following section.
      - Protective layer in finite element method
        When a model with a protective layer is solved using the finite element method, the thermal solver creates 3D elements on top of the selected elements, using defined thickness.
  - Convective heat transfer methods
    The thermal solver computes convection conductances for various geometrical configurations using correlations that depend on specified characteristic lengths, convective surfaces, and type of convection.
  - Radiation exchange methods
    Thermal radiation is a heat transfer due to electromagnetic radiation emitted by the surface of bodies due to their temperature.
  - Miscellaneous topics
  - References
- Thermal solver API guide
  Allows you to create or add functionality to enhance the thermal solver capabilities.

Finite element integration points and shape functions

Integration points and shape functions for different type of elements are predefined in the thermal solver and allow the discretization of a continuous domain and the approximation of its behavior using finite elements.

Integration points are located within each finite element, where the thermal solver performs numerical integration to evaluate the element's temperature. The accuracy of numerical integration directly affects the accuracy of the solution. The element's behavior is expressed in terms of mathematical functions, known as shape function, defined at these integration points. Shape functions, which are expressed as polynomial functions, are used to interpolate the values of the solution field at any point within the element based on known values at the element nodes. Shape functions satisfy properties, such as unity at their corresponding node and zero at other nodes, ensuring accurate interpolation within the element.

The examples show shape functions and graphical representation for supported 2D elements.


Element type	Graphical representation	Shape function
Linear triangle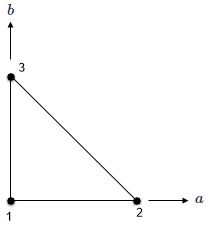
Parabolic triangle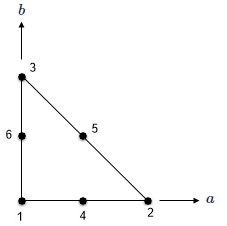
Linear quadrilateral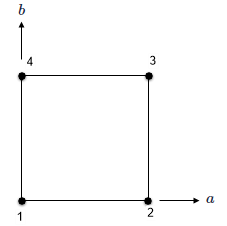
Parabolic quadrilateral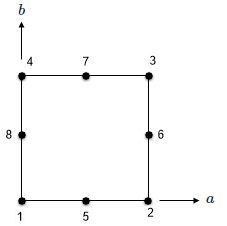
Linear tetrahedron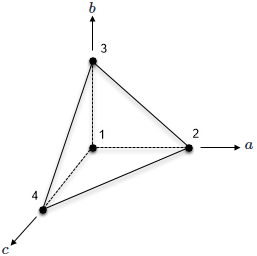
Parabolic tetrahedron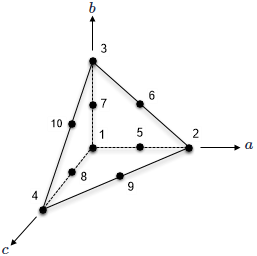