Home
Thermal Solver
Contains thermal solver related guides, such as the TMG reference manual, thermal API guide, and error message list.
Thermal solver theory
Describes the theory and methods of the thermal solver.
Miscellaneous topics
Heat flow calculation between groups B and A using the heat flows through groups
The heat flow between two groups is the sum of the following separate calculations: through directly connected conductances, through conductive conductances with the element CG method, and through Oppenheim radiative conductances.
Radiative heat flow between groups using Oppenheim method
This topic explains the two-step process for calculating radiative heat flow between groups using the Oppenheim method, including the necessary equations and boundary conditions.

Thermal Solver
Contains thermal solver related guides, such as the TMG reference manual, thermal API guide, and error message list.
- Thermal solver guides
  Maya HTT's thermal solver is included in Simcenter 3D and in Simcenter Femap. This page contains links to thermal solver guides, which help you understand how the thermal solver works.
- Thermal solver theory
  Describes the theory and methods of the thermal solver.
  - Introduction
    This guide provides the theory and methods used by the thermal solver, including methods to calculate conduction, convection, and radiation, as well as modeling specific topics using the thermal solver.
  - Conduction methods
    To model heat conduction, the thermal solver can use two finite volume methods, center of element method or element's center of gravity method, or the finite element method.
  - Convective heat transfer methods
    The thermal solver computes convection conductances for various geometrical configurations using correlations that depend on specified characteristic lengths, convective surfaces, and type of convection.
  - Radiation exchange methods
    Thermal radiation is a heat transfer due to electromagnetic radiation emitted by the surface of bodies due to their temperature.
  - Miscellaneous topics
    - Heat flow calculation between groups B and A using the heat flows through groups
      The heat flow between two groups is the sum of the following separate calculations: through directly connected conductances, through conductive conductances with the element CG method, and through Oppenheim radiative conductances.
      - Heat flow between groups through direct conductances
        The heat flow between groups A and B via direct conductances is evaluated by summing the heat flow through all conductances connecting elements of group A and B directly.
      - Heat flow between adjacent groups using the element CG method
        The thermal solver evaluates the conductive heat flow between adjacent groups when the element CG conduction method is used by summing the heat flows across the boundary elements common to groups A and B.
      - Radiative heat flow between groups using Oppenheim method
        This topic explains the two-step process for calculating radiative heat flow between groups using the Oppenheim method, including the necessary equations and boundary conditions.
      - Accuracy issues with the calculation of equivalent conductances and ScriptFij
    - Heat pipe modeling
      Heat pipes transfer heat through the length of a heat pipe, from the evaporator to the condenser, by phase changing a working fluid. The condensed fluid is pumped back to the evaporator by the capillary force in the wick structure.
    - Automatically connected streams
    - Temperature error estimates
  - References
- Thermal solver API guide
  Allows you to create or add functionality to enhance the thermal solver capabilities.

Radiative heat flow between groups using Oppenheim method

This topic explains the two-step process for calculating radiative heat flow between groups using the Oppenheim method, including the necessary equations and boundary conditions.

This calculation is performed in two steps. First, all real element temperatures are set to absolute zero except for those in group B, which are maintained at their calculated values. The temperatures of all Oppenheim elements are then calculated. The radiative heat flow from group B into group A at absolute zero is equal to the heat flow from the Oppenheim conductances of group A into the elements of group A.

Next, the process is reversed: all temperatures, except those in group A, are set to absolute zero. This temperature field is used to compute the radiative heat exchange from group A to B at absolute zero, as explained in the previous step. The net radiative heat flow from B to A is the heat flow calculated in step 1 minus the heat flow calculated in step 2.

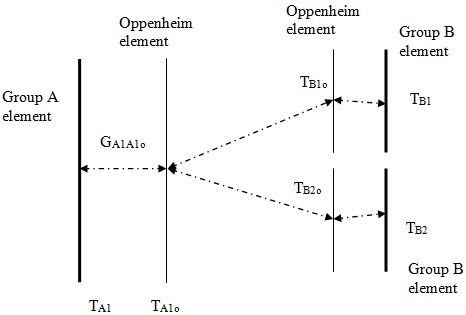
The net heat flow is expressed in the equation below:

where:

Subscript A are elements associated to group A.
Subscript B are elements associated to group B.
Subscript i is the index of elements in group A.
Subscript o are the Oppenheim elements.
Subscript z is the index of element set maintained at absolute zero.
T_Ai is the temperature of the element i in group A.
T_Aio is the temperature of the Oppenheim element of element i in group A.
G_Aio is the conductance between element e_Ai and its Oppenheim element.
T_Aioz is the temperature of the Oppenheim element of e_Ai, the i^th element of group A, calculated with the following BC’s:
- All non-Oppenheim elements (except group B) are sinks with absolute zero temperatures.
- All the B elements are sinks set at their correct temperatures.
T_Bioz is the temperature of the Oppenheim element of e_Bi, the i^th element of group B, calculated with the following BC’s:
- All non-Oppenheim elements (except group A) are sinks with absolute zero temperatures.
- All the A elements are sinks set at their correct temperatures.
G_Bio is the conductance between element e_Bi and its Oppenheim element.