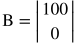Subroutine FASTSOLVE2

Solves the matrix equation AX = B using the iterative biconjugate gradient method, where X is the output vector. The matrix A is created from the contents of arrays icd and cond.

Calling convention:

call fastsolv(icd,cond,icond,itype,isink,par,ierr,x,b)


Arguments	Data type	Input/Output	Description
`icd`	Integer array (2,icond)	Call	Input array of length `icond` that contains the connected element numbers of the conductances specified in `cond`. icd(1,n) is the first element of the I'th conductance. icd(2,n) is the second element of the I'th conductance.
`cond`	Real array (icond)	Call	Conductance value.
`itype`	Integer array (icond)	Call	Specifies conductances type. A value of –1 indictaes that it is a 1-way conductance (only the first element is affected). A value > 0 implies a regular conductance.
`icond`	Integer	Call	The number of conductances in `cond`.
`isink`	Integer array (icond)	Call	If `isink(i)`=1 then element`i`is a boundary condition and takes on the value `b(i)`.
`ierr`	Integer	Return	Error flag. Set to 1 on error, else set to 0.
`par`	Real array (20)	Both	Parameters related to solution. For more information, see the parameter table.
`x`	Real array	Return	The output vector. The array must be greater than the highest element number in array `icd`.
`b`	Real array	Call	The right side input vector. The array must be greater than the highest element number in array `icd`. Contains sink values on input.

Parameter table


Parameter number	Parameter description
1	The input initial fill-in value estimate for the preconditioning matrix. The ILUT preconditioning method is used. `apr(1) = 0` defaults to 7. If convergence is not achieved, the fill-in value is updated in increments of 10 until convergence is achieved. `par(1) = -1` uses the Jacobi preconditioner, where the preconditioning matrix consists of the inverse of the diagonal of the matrix `A`.
2	The input tolerance value specified for eliminating small terms in the preconditioning matrix. `par(2) = 0` defaults to `.0001`.
3	The input convergence criterion. The solution is considered converged if `norm(AX-B)/norm(B)< par (3)`, or if the `par (10)` convergence criterion is fulfilled. `par (3) = 0` defaults to `1.E-8`.
4	The input maximum number of iterations. `par(4) = 0` defaults to `200`.
5	The input flag that prints the convergence residual value to the verbose log file and to the screen. `par(5) = 0` defaults to no residuals printed.
6	Reserved.
7	On return contains the value of the convergence residual.
8	On return contains the number of iterations completed.
9	An input flag to re-use the previously created preconditioning matrix on exit. `par(9) = 0` creates the preconditioning matrix. `par(9) = 1` uses the previously created preconditioning matrix in order to save CPU time.
10	Maximum number of outer loop iterations calling the Conjugate Gradient solver.
11	Input flag to increase performance for repeated re-entry. `par(11) = 1` improves performance by saving all temporary arrays (but not the matrix A) created internally for subsequent re-use. `par(11) = 0` does not save the arrays.
12	An input flag to increase performance for reported re-entry with the same matrix but different `B`. `par(12) = 1` saves all matrices, including the input matrix `A` created from `icd`, for subsequent calculations with another `B` vector.
13	Reserved.
14	Reserved.
15	Reserved.
16	Reserved.
17	Reserved.
18	Reserved.
19	Reserved.
20	Reserved.

The following example solves the matrix AX = B, where the matrices A and B are the following:

The matrix is entered as a sum of 3 conductances: G₂₁ = 1, G₁₂ = 1, and G₁₁ = -1. The second conductance is specified as a 1-way conductance with ITYPE(2) = -1, such that only row 1 is affected, not row 2.

Example:

subroutine user1(gg,t,c,q,qd,r,time,dt,it,
+kode,nocon,maxno,iconv,dum1,dum2,dtp,tf)
dimension t(*),x(4),b(4),par(20),icd(2,2)
dimension cond(2), isink(2),itype(3)
save
data par,x,b,isink,itype/24*0.0,5*0/
icond=3
icd(1,1)=2
icd(2,1)=1
cond(1)=1
icd(1,2)=1
icd(2,2)=2
cond(2)=1
itype(2)=-1
icd(1,3)=1
icd(2,3)=1
cond(3)=-1
b(1)=100
call fastsolve2(icd,cond,icond,itype,isink,par,ierr,x,b)
t(1)=x(1)
t(2)=x(2)
return
end